线段树1

先讲解一下线段树

线段树用于区间操作的优化，来看一道这样的题：

https://www.luogu.org/problem/P2068

在一个序列中，支持以下操作：修改序列中一个数，查询其中y一段区间的和

元素数<=100000,操作数<=10000.

由于数据较大，n*m显然过不了，这时，就要用到线段树了：

这就是线段树示意图

每个节点上都有一个区间，这个节点的点权就是这个区间所有数的和

但不用担心初始化的时间，因为每个节点的点权等于它的左右儿子点权之和

一个节点的左右儿子的点权分别对应l~(l+r)/2的和与(l+r)/2+1~r的和

到叶节点时这个点权就是对应这个数。

所以build就可以这样写

void build(int l,int r,int root)
{
	if(l==r) 
	{
		num[root]=a[l];
		return;
	}
	int mid=(l+r)/2;
	build(l,mid,root*2);
	build(mid+1,r,root*2+1);
	num[root]=min(num[root*2],num[root*2+1]);
}

比如，我要查询的是3~7这个区间，那它的和就是

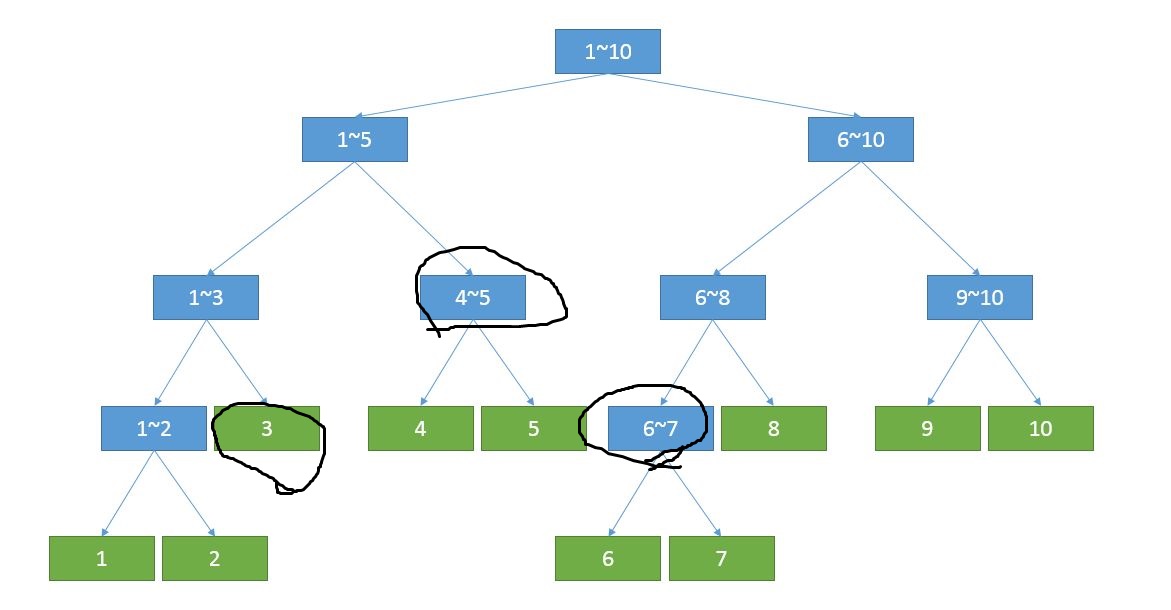
这三个节点的点权之和

现在我们看一下查询的时间复杂度，很明显大约是O（logn）

现在，来看一下查询的代码

int search(int p,int q,int l,int r,int root)
{
	if(p==l && r==q)
	{
		return num[root];
	}
	int mid=(l+r)/2;
	if(p>=mid+1) return search(p,q,mid+1,r,root*2+1);
	else if(q<=mid) return search(p,q,l,mid,root*2);
	else return search(p,mid,l,mid,root*2)+search(mid+1,q,mid+1,r,root*2+1);
}

代码解释

如果要查询的区间被该节点的左子树或右子树完全包含，就只用查找一个子树就行了

否则要查询的区间一定是跨越了两个子树，这样就要查询两次

如果要查询的区间与该节点对应的区间刚好重合，这样就直接return这个值就好了

最后是修改，例如我要修改6这个节点，那要修改的就是

这五个节点，时间复杂度也是O（logn）（因为每层一个）

简单看一下代码

void change(int p,int val,int l,int r,int root)
{
	if(l==r)
	{
		num[root]+=val;
		return;
	}
	int mid=(l+r)/2;
	if(p>=mid+1) change(p,val,mid+1,r,root*2+1);
	else change(p,val,l,mid,root*2);
	num[root]=num[root*2]+num[root*2+1];
}

代码解释

如果要查询的节点再该节点的左子树，就查找一个左子树就行了

否则就查找一个右子树就好了

如果要查询的节点与该节点刚好重合，这样就直接修改这个值就好了

最后是这道题的完整代码

#include<bits/stdc++.h>
using namespace std;
int num[100000*4];
void build(int l,int r,int root)
{
	if(l==r)
	{
		num[root]=0;
		return;
	}
	int mid=(l+r)/2;
	build(l,mid,root*2);
	build(mid+1,r,root*2+1);
	num[root]=num[root*2]+num[root*2+1];
}
void change(int p,int val,int l,int r,int root)
{
	if(l==r)
	{
		num[root]+=val;
		return;
	}
	int mid=(l+r)/2;
	if(p>=mid+1) change(p,val,mid+1,r,root*2+1);
	else change(p,val,l,mid,root*2);
	num[root]=num[root*2]+num[root*2+1];
}
int search(int p,int q,int l,int r,int root)
{
	//printf("%d %d %d %d %d
",p,q,l,r,root);
	if(p==l && r==q)
	{
		return num[root];
	}
	int mid=(l+r)/2;
	if(p>=mid+1) return search(p,q,mid+1,r,root*2+1);
	else if(q<=mid) return search(p,q,l,mid,root*2);
	else return search(p,mid,l,mid,root*2)+search(mid+1,q,mid+1,r,root*2+1);
}
int main()
{
	int n,w;
	scanf("%d%d",&n,&w);
	for(int i=1;i<=w;i++)
	{
		char t;
		int x,y;
		cin>>t>>x>>y;
		if(t=='x')
		{
			change(x,y,1,n,1);
		}
		else if(t=='y')
		{
			printf("%d
",search(x,y,1,n,1));
		}
	}
	return 0;
}

最后再给大家推荐几道线段树的养生的模板题

https://www.luogu.org/problem/U85066

https://www.luogu.org/problem/P1637