题目描述
一个点每过一个单位时间就会向四个方向扩散一个距离,如图。
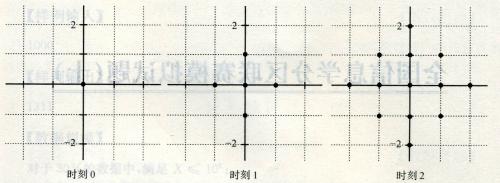
两个点a、b连通,记作e(a,b),当且仅当a、b的扩散区域有公共部分。连通块的定义是块内的任意两个点u、v都必定存在路径e(u,a0),e(a0,a1),…,e(ak,v)。给定平面上的n给点,问最早什么时刻它们形成一个连通块。
输入输出格式
输入格式:
第一行一个数n,以下n行,每行一个点坐标。
【数据规模】
对于20%的数据,满足1≤N≤5; 1≤X[i],Y[i]≤50;
对于100%的数据,满足1≤N≤50; 1≤X[i],Y[i]≤10^9。
输出格式:
一个数,表示最早的时刻所有点形成连通块。
输入输出样例
输入样例#1: 复制
2 0 0 5 5
输出样例#1: 复制
 View Code
View Code
5
二分答案且曼哈顿距离<=mid*2

#include<iostream> #include<cstdio> #include<cmath> using namespace std; int xs[51]; int ys[51];//坐标 int ints[51];//并查集 int find(int n){ if(ints[n]==n)return(n); return(ints[n]=find(ints[n])); } int main(){ int n; cin>>n; for(int i=0;i<n;i++)cin>>xs[i]>>ys[i]; int l=0,r=1000000000; int ans=0;//最终答案 while(l<=r){ int mid=(l+r)>>1;//二分答案 for(register int i=0;i<n;i++){ ints[i]=i; }//初始化并查集 for(register int i=0;i<n;i++){ for(register int j=i+1;j<n;j++){ int dis=abs(xs[i]-xs[j])+abs(ys[i]-ys[j]); if(dis<=mid*2){//能扩散到就连边 int aa=find(i),ab=find(j); if(aa!=ab)ints[aa]=ab; } } } int cnt=0;//连通块个数 for(register int i=0;i<n;i++){ if(ints[i]==i)cnt++; } if(cnt==1){ ans=mid; r=mid-1; }//只有一个连通块就更新答案向下查找 else{ l=mid+1; } } cout<<ans<<endl; return(0); }
