In this problem, we will define a graph called star graph, and the question is to find the minimum distance between two given nodes in the star graph.
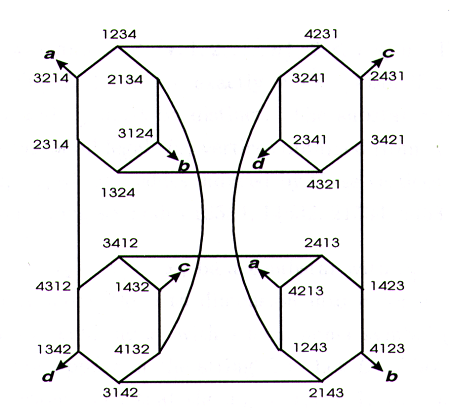
Given an integer n, an n−dimensionalstar graph, also referred to as Sn, is an undirected graph consisting of n! nodes (or vertices) and ((n−1) ∗ n!)/2 edges. Each node is uniquely assigned a label x1 x2 ... xnwhich is any permutation of the n digits 1,2,3,...,n. For instance, an S4 has the following 24 nodes 1234,1243,1324,1342,1423,1432,2134,2143,2314,2341,2413,2431,3124,3142,3214,3241,3412,3421,4123,4132,4213,4231,4312,4321. For each node with label x1 x2x3 x4 ... xn, it has n−1 edges connecting to nodes x2 x1 x3 x4 ... xn, x3 x2 x1 x4 ... xn, x4 x2 x3 x1 ... xn, ..., and xn x2 x3 x4 ... x1. That is, the n−1 adjacent nodes are obtained by swapping the first symbol and the d−th symbol of x1 x2 x3 x4 ... xn, for d=2,...,n. For instance, in S4, node 1234has 3 edges connecting to nodes 2134, 3214, and 4231. The following figure shows how S4looks (note that the symbols a, b, c, and d are not nodes; we only use them to show the connectivity between nodes; this is for the clarity of the figure).
In this problem, you are given the following inputs:
- n: the dimension of the star graph. We assume that n ranges from 4 to 9.
- Two nodes x1 x2 x3 ... xn and y1 y2 y3 ... yn in Sn.
You have to calculate the distance between these two nodes (which is an integer).
Input Format
n (dimension of the star graph)
A list of 5 pairs of nodes.
Output Format
A list of 5 values, each representing the distance of a pair of nodes.
样例输入
4 1234 4231 1234 3124 2341 1324 3214 4213 3214 2143
样例输出
1 2 2 1 3
题目来源
题意:给你1-N的N个数,构建N维(几维其实不重要),然后构图的规则是相邻的顶点只能是由第一个字符跟2-n的字符进行交换得来的,问你给出的五个询问中两个节点的最短距离分别是多少?
思路:宽度优先搜索加剪枝,对搜过的节点进行弹出
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string.h>
#include<string>
#include<set>
#include<queue>
using namespace std;
string numa;
string numb;
int n;
struct node{
string str;
int times;
};
int bfs() {
queue<node> q;
set<string> ss;
node now,next;
now.str = numa;
now.times = 0;
q.push(now);
ss.insert(now.str);
while (!q.empty()) {
now = q.front();
q.pop();
if (now.str == numb)
return now.times;
for (int i = 1; i < n; ++i) {
next.str = now.str;
next.times=now.times+1;
next.str[i] = now.str[0];
next.str[0] = now.str[i];
if (ss.count(next.str) == 0)
{
ss.insert(next.str);
q.push(next);
}else
continue;
}
}
}
int main()
{
scanf("%d", &n);
int t = 5;
while (t--) {
cin >> numa >> numb;
cout << bfs() << endl;
}
return 0;
}