统计学习方法c++实现之二 k近邻算法
前言
k近邻算法可以说概念上很简单,即:“给定一个训练数据集,对新的输入实例,在训练数据集中找到与这个实例最邻近的k个实例,这k个实例的多数属于某个类,就把该输入分为这个类。”其中我认为距离度量最关键,但是距离度量的方法也很简单,最长用的就是欧氏距离,其他的距离度量准则实际上就是不同的向量范数,这部分我就不赘述了,毕竟这系列博客的重点是实现。代码地址:https://github.com/bBobxx/statistical-learning
kd树
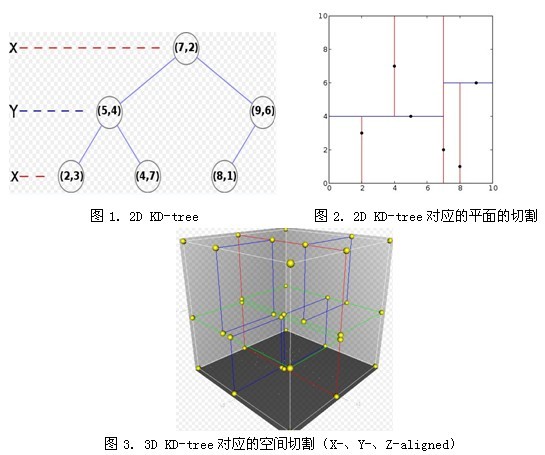
k近邻算法的思想很简单,然而,再简单的概念如果碰上高维度加上海量数据,就变得很麻烦,如果按照常规思想,将每个测试样本和训练样本的距离算出来,在进行排序查找,无疑效率十分低下,这也就是为什么要介绍kd树的原因。kd树是一种二叉树,kd树的每个结点对应一个k维超矩形区域。 kd树的k是k维空间,k近邻算法的k是k个最近值,不是一样的!看文字很抽象,其实很好理解,看图
代码结构
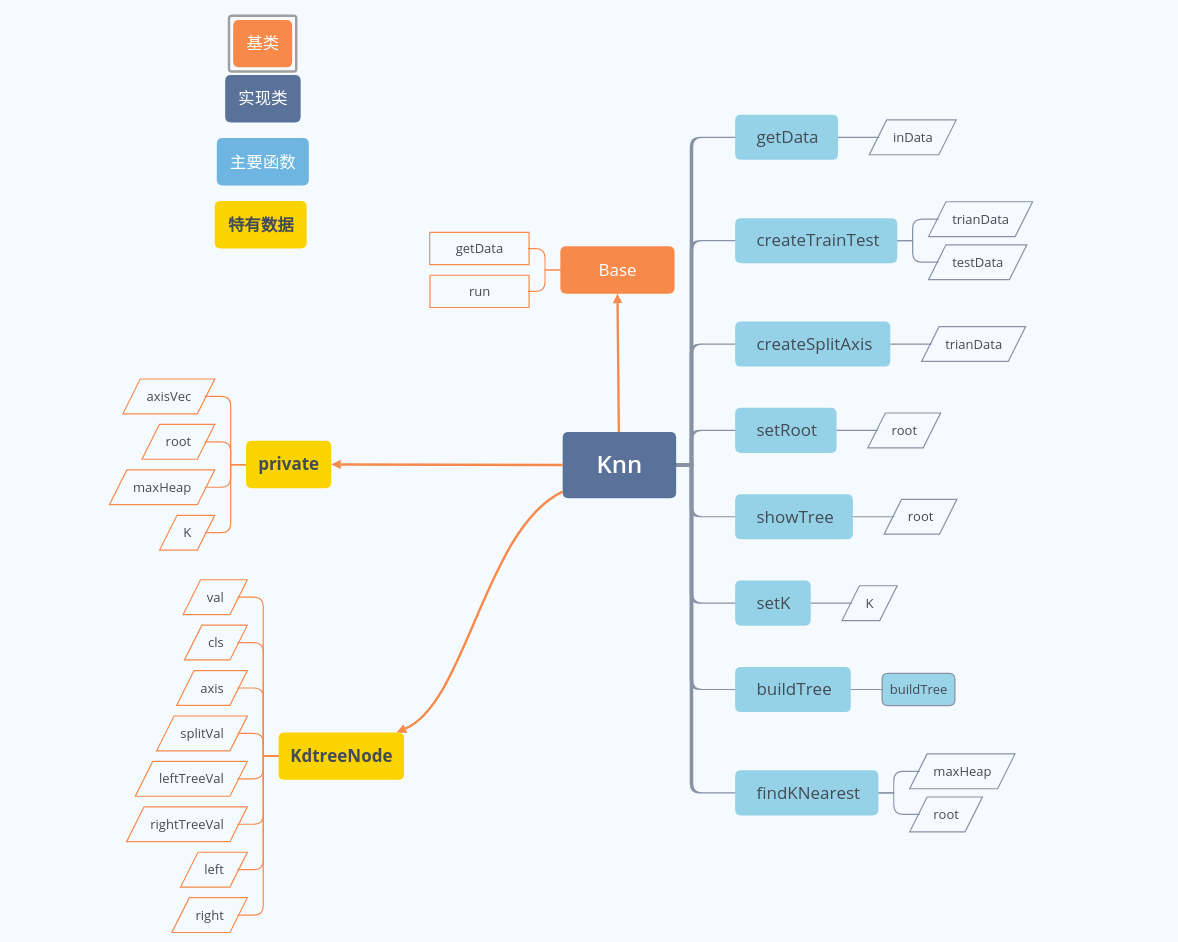
实现
kd树构建代码
每一次分割都需要确定一个轴和一个值,然后分割时只看该轴的数据,小于等于分割值就放到该结点的左子树里,大于分割值就放到右子树中。那么每个结点里面需要存储哪些内容呢?
我的实现里面,每个结点有如下内容:
struct KdtreeNode {
vector<double> val;//n维特征
int cls;//类别
unsigned long axis;//分割轴
double splitVal;//分割的值
vector<vector<double>> leftTreeVal;//左子树的值集合
vector<vector<double>> rightTreeVal;//右子树的值集合
KdtreeNode* parent;//父节点
KdtreeNode* left;//左子节点
KdtreeNode* right;//右子节点
KdtreeNode(): cls(0), axis(0), splitVal(0.0), parent(nullptr), left(nullptr), right(nullptr){};
};
用kd树实现的k近邻算法(还有其它的方法),训练过程实际上就是树的建造过程,我们用递归创建kd树。
首先,我们需要创建并存储根节点
KdtreeNode* root = new KdtreeNode();//类中用这个存储根节点
void Knn::setRoot() {//这是创建根节点的程序,主要是设定左右子树,还有分割轴,分割值
if(axisVec.empty()){
cout<<"please run createSplitAxis first."<<endl;
throw axisVec.empty();
}
auto axisv = axisVec;
auto axis = axisv.top();
axisv.pop();
std::sort(trainData.begin(), trainData.end(), [&axis](vector<double> &left, vector<double > &right) {
return left[axis]<right[axis];
});
unsigned long mid = trainData.size()/2;
for(unsigned long i = 0; i < trainData.size(); ++i){
if(i!=mid){
if (i<mid)
root->leftTreeVal.push_back(trainData[i]);
else
root->rightTreeVal.push_back(trainData[i]);
} else{
root->val.assign(trainData[i].begin(),trainData[i].end()-1);
root->splitVal = trainData[i][axis];
root->axis = axis;
root->cls = *(trainData[i].end()-1);
}
}
cout<<"root node set over"<<endl;
}
上面的程序创建了根节点,但是分割轴是怎么确定?当然可以依次选轴作为分割轴,但是这里我们选择按方差从大到小的顺序选轴
stack<unsigned long> axisVec;//用栈存储分割轴,栈顶轴方差最大。
void Knn::createSplitAxis(){//axisVec创建代码
cout<<"createSplitAxis..."<<endl;
//the last element of trainData is gt
vector<pair<unsigned long, double>> varianceVec;
auto sumv = trainData[0];
for(unsigned long i=1;i<trainData.size();++i){
sumv = sumv + trainData[i];
}
auto meanv = sumv/trainData.size();
vector<decltype(trainData[0]-meanv)> subMean;
for(const auto& c:trainData)
subMean.push_back(c-meanv);
for (unsigned long i = 0; i < trainData.size(); ++i) {
for (unsigned long j = 0; j < indim; ++j) {
subMean[i][j] *= subMean[i][j];
}
}
auto varc = subMean[0];
for(unsigned long i=1;i<subMean.size();++i){
varc = varc + subMean[i];
}
auto var = varc/subMean.size();
for(unsigned long i=0;i<var.size()-1;++i){//here not contain the axis of gt
varianceVec.push_back(pair<unsigned long, double>(i, var[i]));
}
std::sort(varianceVec.begin(), varianceVec.end(), [](pair<unsigned long, double> &left, pair<unsigned long, double> &right) {
return left.second < right.second;
});
for(const auto& variance:varianceVec){
axisVec.push(variance.first);//the maximum variance is on the top
}
cout<<"createSplitAxis over"<<endl;
}
现在要给根节点添加左右子树:
root->left = buildTree(root, root->leftTreeVal, axisVec);
root->right = buildTree(root, root->rightTreeVal, axisVec);
来看一下buildTree代码:
KdtreeNode* Knn::buildTree(KdtreeNode*root, vector<vector<double>>& data, stack<unsigned long>& axisStack) {//第一个参数是父节点,第二个参数是目前没有被分割的数据集合,第三个参数是当前的轴栈,
//由于后面要保证左右子树的分割用的同一个轴,所以这里要传入。
stack<unsigned long> aS;
if(axisStack.empty())
aS=axisVec;
else
aS=axisStack;
auto node = new KdtreeNode();
node->parent = root;
auto axis2 = aS.top();
aS.pop();
std::sort(data.begin(), data.end(), [&axis2](vector<double> &left, vector<double > &right) {
return left[axis2]<right[axis2];
});//这里用的c++11里面的lambda函数
unsigned long mid = data.size()/2;
if(node->leftTreeVal.empty()&&node->rightTreeVal.empty()){
for(unsigned long i = 0; i < data.size(); ++i){
if(i!=mid){
if (i<mid)
node->leftTreeVal.push_back(data[i]);
else
node->rightTreeVal.push_back(data[i]);
} else{
node->val.assign(data[i].begin(),data[i].end()-1);
node->splitVal = data[i][axis2];
node->axis = axis2;
node->cls = *(data[i].end()-1);
}
}
}
if(!node->leftTreeVal.empty()){
node->left = buildTree(node, node->leftTreeVal, aS);//递归建立子树
}
if(!node->rightTreeVal.empty()){
node->right = buildTree(node, node->rightTreeVal, aS);
}
return node;
}
建立好子树后可以通过showTree函数前序遍历树来查看,这里就不演示了,代码中有这一步。
查找K近邻
对于用kd树实现的Knn算法来说,预测的过程就是查找的过程,这里我们给出查找K个最近邻的代码,中间用到了STL标准模板库的priority_queue和pair的组合,用priority_queue实现大顶堆,对于由pair构成的priority_queue来说,默认的比较值是first,也就是说里面的元素会根据pair的第一个元素从大到小排序,即用.top()得到的是最大值(默认比较函数的情况下)。在搜索 K-近邻时,设置一个有 k 个元素的大顶堆,建立树时,当堆不满时,将结点和距离放入,堆满时,只需比较当前搜索点的 dis 是否小于堆顶点的 dis,如果小于,堆顶出堆,并将当前搜索点压入。
priority_queue<pair<double, KdtreeNode*>> maxHeap;
下面给出查找代码
void Knn::findKNearest(vector<double>& testD){
...//前面略过,避免代码过长。。。
if(testDF[curNparent->axis]<=curNparent->splitVal)//从这里开始是为了查找同一个父节点的
//另一个子树中是否有比当前K个最近邻更近的结点
curNchild = curNparent->right;//这里和上面相反,刚好是另一个子树。
else
curNchild = curNparent->left;
if(curNchild == nullptr)
continue;
double childDis = computeDis(testDF, curNchild->val);
if(childDis<maxHeap.top().first){//比较另一个子树的根节点是不是比当前k个结点距离查找点更近,
//如果是,将对应的子树加入搜索路径
maxHeap.pop();
maxHeap.push(pair<double, KdtreeNode*>(childDis, curNchild));
while(curNchild!= nullptr){//add subtree to path
path.push(curNchild);
if(testD[curNchild->axis]<=curNchild->splitVal)
curNchild = curNchild->left;
else
curNchild = curNchild->right;
}
}
}
}
double Knn::computeDis(const vector<double>& v1, const vector<double>& v2){
auto v = v1 - v2;
double di = v*v;//这里用到了基类中的操作符重载
return di;
}
总结
k近邻算法虽然概念简单,但是实现由于要用到树结构,编写起来还是挺具有挑战性的,以后还会进行性能的优化,慢慢来。