zkw线段树是一种用空间换取操作的简便性和时间常数的线段树。
它使线段树节点的存储位置有规律,从而将线段树的递归操作用循环替代
zkw线段树一般分为有区间修改和无区间修改两种,无区间修改的zkw线段树可以做到O(1)的单点查询,比有区间修改的要快
无区间修改的zkw线段树
建树
下面用一张图解释普通线段树和zkw线段树区别
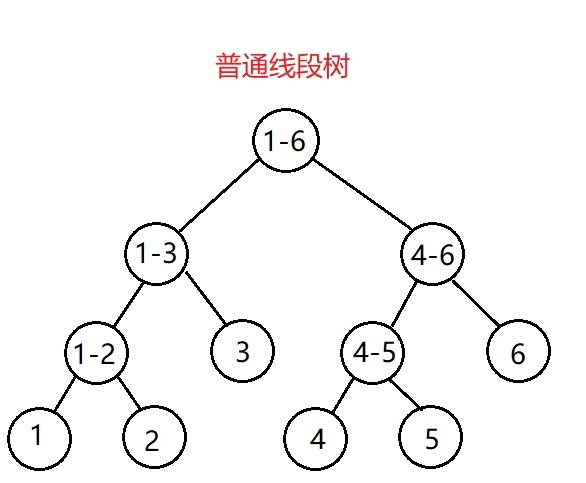
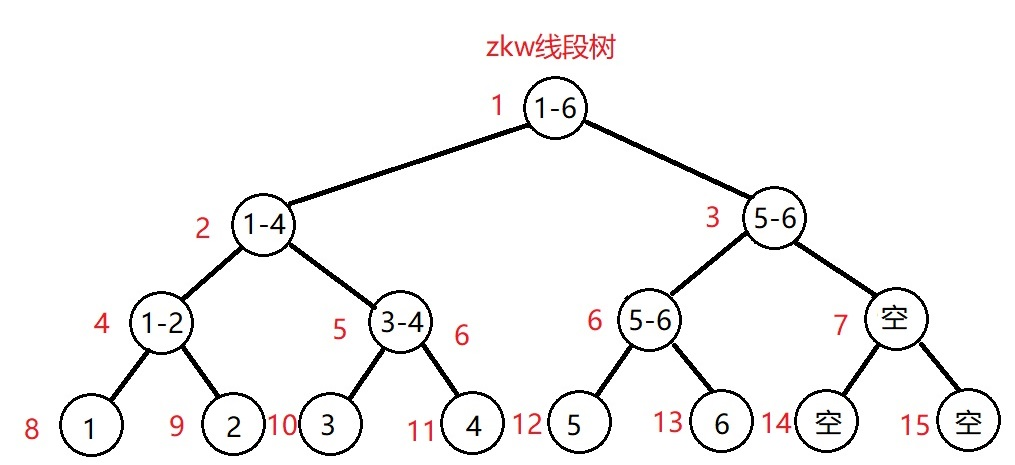
我们发现zkw线段树是一棵完全二叉树,它的左右儿子的编号分别为父节点的2倍和2倍+1,并且叶子节点都在同一层
因为构造这棵完全二叉树会空出一些节点,所以节点数量要开到第一个>=n*2的2次幂(如果不计算可直接开到n*4)
void build(int n){//建树 M=1;while((M<<=1)<n); M--; for(int i=1;i<=n;i++)ma[i+M]=a[i]; for(int i=M;i;i--){ ma[i]=max(ma[i<<1],ma[i<<1|1]); } }
单点修改
因为所有子节点都连续,所有直接找到子节点,修改后再向上更新祖先即可
void update(int x){//向上更新 while((x<<=1)){ ma[x]=max(ma[x<<1],ma[x<<1|1]); } } void change_val(int x,int y){//单点修改 ma[x+M]=y; update(x+M); }
单点查询
因为子节点连续,所以可以直接找到位置输出
int query_node(int x){//单点查询 return ma[x+M]; }
区间查询
如果区间的左右端点不是同一个父节点,
那么如果左端点是左子节点,则对应右子节点一定全在区间中,更新询问的值即可
同理如果右端点是右子节点,则对应左子节点一定全在区间中,同理,更新询问值
将左右端点变作自己的父亲,继续第一步的判断
如果区间的左右端点是同一个父节点,则所有区间都被统计了,直接返回即可
int query(int l,int r){//区间查询 int ans=0; for(l=l+M-1,r=r+M+1;l^r^1;l>>=1,r>>=1){ if(~l&1)ans=max(ma[l^1],ans); if(r&1)ans=max(ma[r^1],ans); } return ans; }
模板
-
维护区间和
void build(int n){//建树 M=1;while((M<<=1)<n); M--; for(int i=1;i<=n;i++)sum[i+M]=a[i]; for(int i=M;i;i--){ sum[i]=sum[i<<1]+sum[i<<1|1]; } } void change(int x,int y){//单点修改 x+=M; sum[x]+=y; while((x>>=1)){ sum[x]+=y; } } int query_node(int x){//单点查询 return sum[x+M]; } int query(int l,int r){//区间查询 int ans=0; for(l=l+M-1,r=r+M+1;l^r^1;l>>=1,r>>=1){ if(~l&1)ans+=sum[l^1]; if(r&1)ans+=sum[r^1]; } return ans; }
-
维护最值
void build(int n){//建树 M=1;while((M<<=1)<n); M--; for(int i=1;i<=n;i++)ma[i+M]=a[i]; for(int i=M;i;i--){ ma[i]=max(ma[i<<1],ma[i<<1|1]); } } void update(int x){//向上更新 while((x>>=1)){ ma[x]=max(ma[x<<1],ma[x<<1|1]); } } void change_val(int x,int y){//单点修改 ma[x+M]=y; update(x+M); } int query_node(int x){//单点查询 return ma[x+M]; } int query(int l,int r){//区间查询 int ans=0; for(l=l+M-1,r=r+M+1;l^r^1;l>>=1,r>>=1){ if(~l&1)ans=max(ma[l^1],ans); if(r&1)ans=max(ma[r^1],ans); } return ans; }
例题
#include<cstdio> #include<algorithm> using namespace std; #define maxn 10000005 int ma[maxn<<2],a[maxn],M; void build(int n){//建树 M=1;while((M<<=1)<n); M--; for(int i=1;i<=n;i++)ma[i+M]=a[i]; for(int i=M;i;i--){ ma[i]=max(ma[i<<1],ma[i<<1|1]); } } void update(int x){//向上更新 while((x<<=1)){ ma[x]=max(ma[x<<1],ma[x<<1|1]); } } void change_val(int x,int y){//单点修改 ma[x+M]=y; update(x+M); } int query_node(int x){//单点查询 return ma[x+M]; } int query(int l,int r){//区间查询 int ans=0; for(l=l+M-1,r=r+M+1;l^r^1;l>>=1,r>>=1){ if(~l&1)ans=max(ma[l^1],ans); if(r&1)ans=max(ma[r^1],ans); } return ans; } int main(){ freopen("climb.in","r",stdin); freopen("climb.out","w",stdout); int n,q,l,r;scanf("%d",&n),n++; for(int i=1;i<=n;i++)scanf("%d",a+i); build(n); scanf("%d",&q); for(int i=0;i<q;i++){ scanf("%d%d",&l,&r); printf("%d ",query(l+1,r+1)); } return 0; }
带区间修改的zkw线段树
-
维护区间和
维护区间和的zkw线段树我们和普通线段树一样打lazy标记
建树和单点修改(同无区间修改)
void build(int n){//建树 M=1;while((M<<=1)<n); M--; for(int i=1;i<=n;i++){ sum[i+M]=a[i]; } for(int i=M;i>0;i--){ sum[i]=sum[i<<1]+sum[i<<1|1]; } } void change(int x,int y){//单点修改 x+=M; sum[x]+=y; while(x>>=1){ sum[x]+=y; } }
区间修改
区间修改的操作利用了上面区间查询的思想
如果区间的左右端点不是同一个父节点,
那么如果左端点是左子节点,则对应右子节点一定全在区间中,这时对右子节点打lazy标记,更新右子节点的sum
同理如果右端点是右子节点,则对应左子节点一定全在区间中,对左子节点打lazy标记,更新维护的值
将左右端点变作自己的父亲,继续第一步的判断当区间的左右端点是同一个父节点时,就没有lazy标记了,直接向上更新到根的路径上的节点即可
void modify(int l,int r,int w){//区间修改 if(l==r){change(l,w);return;} int d=1; sum[l+M]+=w,sum[r+M]+=w;//注:下面的操作不会更新端点的值,所以提前将端点更新 for(l+=M,r+=M;l^r^1;l>>=1,r>>=1){ if(~l&1)sum[l^1]+=w*d,lazy[l^1]+=w;//在对应的右子节点打个标记,更新sum的值 if(r&1)sum[r^1]+=w*d,lazy[r^1]+=w;//在对应的左子节点打个标记,更新sum的值 d<<=1; sum[l>>1]=sum[l]+sum[l^1]+lazy[l>>1]*d;//更新两个父节点的值,其中d表示父节点表示区间的长度 sum[r>>1]=sum[r]+sum[r^1]+lazy[r>>1]*d; } while(l>>=1)d<<=1,sum[l]=sum[l<<1]+sum[l<<1|1]+lazy[l]*d;//更新路径上节点的sum值 }
单点查询
查询叶子节点的值,然后加上到根节点的路径中的lazy标记即可
int query_node(int l){//单点查询 int x=l+M,ans=0; while(x>>=1){ if(lazy[x])ans+=lazy[x]; } return sum[l+M]+ans; }
区间查询
由于统计时是由底部向顶部进行查询
所以我们不像普通线段树那样下放lazy标记,而是在向上过程中统计lazy标记造成的影响代码大体和无区间修改的差不多
LL query(int l,int r){//区间查询 (区间和) int L=0,R=0,d=1;//L,R分别记录所求区间中有多少个节点处于左右端点所在的节点中,d记录所在层次的节点代表的区间长度 LL ans=0; for(l=l+M-1,r=r+M+1;l^r^1;l>>=1,r>>=1){ if(lazy[l])ans+=L*lazy[l];//计算lazy[l]影响的值 if(lazy[r])ans+=R*lazy[r];//计算lazy[r]影响的值 if(~l&1)ans+=sum[l^1],L+=d;//左端点所在的点是左子节点,则对应的右子节点处于区间中,更新L的值 if(r&1)ans+=sum[r^1],R+=d; d<<=1; } ans+=lazy[l]*L,ans+=lazy[r]*R,L+=R; while(l>>=1){//计算路径上的lazy造成的影响 if(lazy[l])ans+=lazy[l]*L; } return ans; }
例题P3372 【模板】线段树 1
#include<cstdio> #include<algorithm> using namespace std; #define maxn 100005 #define LL long long LL sum[maxn<<2],a[maxn],M,lazy[maxn<<2],k; void build(int n){//建树 M=1;while((M<<=1)<n); M--; for(int i=1;i<=n;i++){ sum[i+M]=a[i]; } for(int i=M;i>0;i--){ sum[i]=sum[i<<1]+sum[i<<1|1]; } } void change(int x,int y){//单点修改 x+=M; sum[x]+=y; while(x>>=1){ sum[x]+=y; } } void modify(int l,int r,int w){//区间修改 if(l==r){change(l,w);return;} int d=1; sum[l+M]+=w,sum[r+M]+=w;//注:下面的操作不会更新端点的值,所以提前将端点更新 for(l+=M,r+=M;l^r^1;l>>=1,r>>=1){ if(~l&1)sum[l^1]+=w*d,lazy[l^1]+=w;//在对应的右子节点打个标记,更新sum的值 if(r&1)sum[r^1]+=w*d,lazy[r^1]+=w;//在对应的左子节点打个标记,更新sum的值 d<<=1; sum[l>>1]=sum[l]+sum[l^1]+lazy[l>>1]*d;//更新两个父节点的值,其中d表示父节点表示区间的长度 sum[r>>1]=sum[r]+sum[r^1]+lazy[r>>1]*d; } while(l>>=1)d<<=1,sum[l]=sum[l<<1]+sum[l<<1|1]+lazy[l]*d;//更新路径上节点的sum值 } int query_node(int l){//单点查询 int x=l+M,ans=0; while(x>>=1){ if(lazy[x])ans+=lazy[x]; } return sum[l+M]+ans; } LL query(int l,int r){//区间查询 (区间和) int L=0,R=0,d=1;//L,R分别记录所求区间中有多少个节点处于左右端点所在的节点中,d记录所在层次的节点代表的区间长度 LL ans=0; for(l=l+M-1,r=r+M+1;l^r^1;l>>=1,r>>=1){ if(lazy[l])ans+=L*lazy[l];//计算lazy[l]影响的值 if(lazy[r])ans+=R*lazy[r];//计算lazy[r]影响的值 if(~l&1)ans+=sum[l^1],L+=d;//左端点所在的点是左子节点,则对应的右子节点处于区间中,更新L的值 if(r&1)ans+=sum[r^1],R+=d; d<<=1; } ans+=lazy[l]*L,ans+=lazy[r]*R,L+=R; while(l>>=1){//计算路径上的lazy造成的影响 if(lazy[l])ans+=lazy[l]*L; } return ans; } int main(){ int n,q,x,l,r;scanf("%d%d",&n,&q); for(int i=1;i<=n;i++)scanf("%lld",a+i); build(n); for(int i=0;i<q;i++){ scanf("%d",&x); if(x==1){ scanf("%d%d%lld",&l,&r,&k); modify(l,r,k); } else{ scanf("%d%d",&l,&r); printf("%lld ",query(l,r)); } } return 0; }
-
维护最大值
维护最大值时可以不用lazy标记,但需要用到差分思想,即每个节点只存储与父节点的差值
建树
和无区间修改的建树差不多,只是每个节点最后要减去父节点的值
void build(int n){//建树 M=1; while((M<<=1)<n); M--; for(int i=0;i<n;i++){ mi[i+M]=a[i]; } for(int i=M;i;i--){ mi[i]=min(mi[i<<1],mi[i<<1|1]); mi[i<<1]-=mi[i],mi[i<<1|1]-=mi[i];//节点存储与父节点的差值 } }
单点修改
和无区间修改的基本一样,只是更新父节点方法不同
void change(int x,int w){//单点修改 x+=M;mi[x]+=w; int tmp; while(x>>=1){//更新祖先的值 tmp=min(mi[x<<1],mi[x<<1|1]); mi[x]+=tmp,mi[x<<1]-=tmp,mi[x<<1|1]-=tmp; } }
区间修改
还是利用的区间查询的那种思想
如果区间的左右端点不是同一个父节点,
那么如果左端点是左子节点,则对应右子节点一定全在区间中,更新右子节点
同理如果右端点是右子节点,则对应左子节点一定全在区间中,更新左子节点
更新它们的父亲节点并将左右端点变作自己的父亲,继续第一步的判断当区间的左右端点是同一个父节点时,直接向上更新到根的路径上的节点即可
void modify(int l,int r,int w){//区间修改 int tmp; for(l+=M-1,r+=M+1;l^r^1;l>>=1,r>>=1){ if(~l&1)mi[l^1]+=w;//如果为左端为左子节点,则右子节点一定被包含,更新值 if(r&1)mi[r^1]+=w;//如果为右端为右子节点同理 tmp=min(mi[l],mi[l^1]),mi[l]-=tmp,mi[l^1]-=tmp,mi[l>>1]+=tmp;//更新左右端父节点的值 tmp=min(mi[r],mi[r^1]),mi[r]-=tmp,mi[r^1]-=tmp,mi[r>>1]+=tmp; } while(l>>=1){//更新到根的路径的值 tmp=min(mi[l<<1],mi[l<<1|1]),mi[l<<1]-=tmp,mi[l<<1|1]-=tmp,mi[l]+=tmp; } }
单点查询
找到叶子节点,答案就是它到根节点路径上值的和
int query_node(int x){//单点查询 x+=M; int ans=mi[x]; while(x>>=1)ans+=mi[x];//因为存的为与父节点的差,所以答案要加上所有路径上的点的值 return ans; }
区间查询
用两个整数L,R记录左右端点所在节点表示的区间与所求区间交集的最小值(最小值是与父亲的差值)
如果区间的左右端点不是同一个父节点,更新这两个整数
那么如果左端点是左子节点,则对应右子节点一定全在区间中,用它更新L的值
同理如果右端点是右子节点,则对应左子节点一定全在区间中,用它更新R的值
将左右端点变作自己的父亲,继续第一步的判断当区间的左右端点是同一个父节点时,合并L,R,然后加上到根节点路径上的值
int query(int l,int r){//区间查询 if(l==r)return query_node(l);//特判单点查询,否则会死循环 int ans,L=0,R=0; for(l+=M,r+=M;l^r^1;l>>=1,r>>=1){ L+=mi[l],R+=mi[r];//L,R表示左右端点所在节点表示的区间与所求区间交集的最小值 if(~l&1)L=min(L,mi[l^1]);//如果为左端为左子节点,则右子节点一定被包含,更新值 if(r&1)R=min(R,mi[r^1]);//如果为右端为右子节点同理 } L+=mi[l],R+=mi[r],ans=min(L,R);//答案要加上路径上所有的点的值 while(l>>=1){ ans+=mi[l]; } return ans; }
例题codevs1291 火车线路
#include<cstdio> #include<algorithm> using namespace std; #define maxn 1<<17 #define inf 0x3fffffff int mi[maxn],M,s,a[maxn]; void build(int n){ M=1; while((M<<=1)<n); M--; for(int i=0;i<n;i++){ mi[i+M]=a[i]; } for(int i=M;i;i--){ mi[i]=min(mi[i<<1],mi[i<<1|1]); mi[i<<1]-=mi[i],mi[i<<1|1]-=mi[i]; } } void change(int x,int w){ x+=M;mi[x]+=w; int tmp; while(x>>=1){ tmp=min(mi[x<<1],mi[x<<1|1]); mi[x]+=tmp,mi[x<<1]-=tmp,mi[x<<1|1]-=tmp; } } void modify(int l,int r,int w){ if(l==r){change(l,w);return;} int tmp; mi[l+M]+=w,mi[r+M]+=w; for(l+=M,r+=M;l^r^1;l>>=1,r>>=1){ if(~l&1)mi[l^1]+=w; if(r&1)mi[r^1]+=w; tmp=min(mi[l],mi[l^1]),mi[l]-=tmp,mi[l^1]-=tmp,mi[l>>1]+=tmp; tmp=min(mi[r],mi[r^1]),mi[r]-=tmp,mi[r^1]-=tmp,mi[r>>1]+=tmp; } while(l>>=1){ tmp=min(mi[l<<1],mi[l<<1|1]),mi[l<<1]-=tmp,mi[l<<1|1]-=tmp,mi[l]+=tmp; } } int query_node(int x){ x+=M; int ans=mi[x]; while(x>>=1)ans+=mi[x]; return ans; } int query(int l,int r){ if(l==r)return query_node(l); int ans,L=0,R=0; for(l+=M,r+=M;l^r^1;l>>=1,r>>=1){ L+=mi[l],R+=mi[r]; if(~l&1)L=min(L,mi[l^1]); if(r&1)R=min(R,mi[r^1]); } L+=mi[l],R+=mi[r],ans=min(L,R); while(l>>=1){ ans+=mi[l]; } return ans; } int main(){ int n,m,l,r,w,x;scanf("%d%d%d",&n,&s,&m); build(n); for(int i=0;i<m;i++){ scanf("%d%d%d",&l,&r,&w); x=query(l,r-1); if(x<w)printf("N "); else{ printf("T "); modify(l,r-1,-w); } } return 0; }