定义:
有两组单调数列
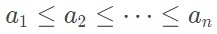
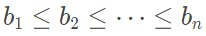
有
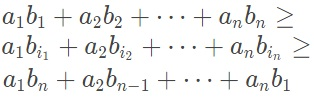
(顺序和>=乱序和>=逆序和)
![]() 是
是![]() 的一个全排列
的一个全排列
并且相等的情况为对应交换的元素是相等的
如:![]() ,其他
,其他![]() 时,只有
时,只有![]() 时
时
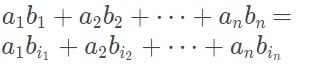
证明:
对于任意
![]()
如果不是完全逆序,我们找到![]()
交换ax,ay,两个式子的差值为![]()
化简得![]()
逆序和是唯一找不到这对数的序列,所以最小,
所有乱序和都可以由顺序和经过一些这样的变换得到,所以顺序和最大
证明完毕
有两组单调数列
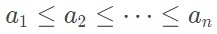
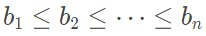
有
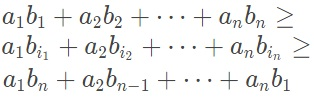
(顺序和>=乱序和>=逆序和)
![]() 是
是![]() 的一个全排列
的一个全排列
并且相等的情况为对应交换的元素是相等的
如:![]() ,其他
,其他![]() 时,只有
时,只有![]() 时
时
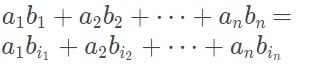
对于任意
![]()
如果不是完全逆序,我们找到![]()
交换ax,ay,两个式子的差值为![]()
化简得![]()
逆序和是唯一找不到这对数的序列,所以最小,
所有乱序和都可以由顺序和经过一些这样的变换得到,所以顺序和最大
证明完毕