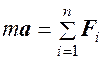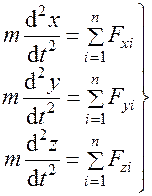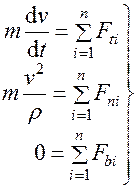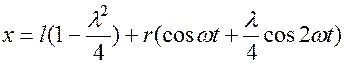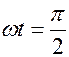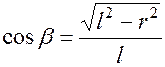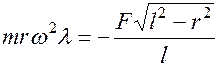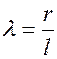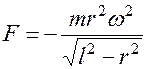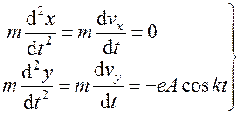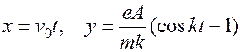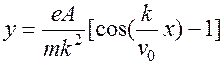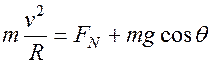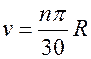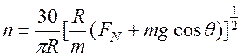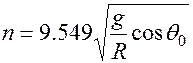§11-2 质点的运动微分方程
1. 矢量形式的运动微分方程
(1)运动微分方程
质点受几个力F1,F2,…,Fn作用时,矢量形
式的运动微分方程为
(2)运动微分方程的另一矢量形式
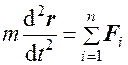 |
(10-3a)
2. 微分方程在直角坐标轴上的投影
(1)力在直角坐标轴上的投影
在计算实际问题时,需要应用式(10-3a)的投
影形式。
设矢径r在直角坐标轴上的投影分别为x,y,z,力F在直角坐标轴上的投影分别为Fxi,Fyi,Fzi。
(2)直角坐标投影表达式
式(10-3a)在直角坐标轴上的投影为
3. 微分方程在自然轴上的投影
(1)点的全加速度
点的全加速度a在切线与主法线构成的密切面内,点的加速度在副法线上的投影等于零,即
式中![]() 和n分别是沿轨迹切线和主法线的单位矢量,如图10-1所示。
和n分别是沿轨迹切线和主法线的单位矢量,如图10-1所示。
图10-1
(2)自然轴系上的投影式
式(10-3)在自然轴系上的投影式为
式中Fti,Fni,Fbi分别是作用于质点上各力在切线、主法线和副法线上的投影,![]() 是轨迹的曲率半径。
是轨迹的曲率半径。
4. 质点动力学的两类基本问题
(1)第一类基本问题
第一类基本问题是:已知质点的运动,求作用于质点的力。
对于第一类基本问题,只需对质点已知的运动方程求两次导数,得到质点的加速度,代入质点的运
动微分方程,即可求解第一类基本问题。
(2)第二类基本问题
第二类基本问题是:已知作用于质点的力,求
质点的运动。
对于第二类基本问题,是解微分方程,即按作
用力的函数规律进行积分,并根据问题的具体运动条件确定积分常数。
5. 例题
例10-1
曲柄连杆机构如图10-2a所示。曲柄OA以匀角速度![]() 转动,OA = r,AB = l,当
转动,OA = r,AB = l,当![]() 比较小时,以O为坐标原点,滑块B的运动方程可近似写为
比较小时,以O为坐标原点,滑块B的运动方程可近似写为
如滑块的质量为m,忽略摩擦及连杆AB的质量,求当![]() 和
和![]() 时,连杆AB所受的力。
时,连杆AB所受的力。
图10-2
解:
该问题属于动力学第一类基本问题。以滑块B为研究对象,当![]() 时,受力如图所示。
时,受力如图所示。
滑块B沿x轴的运动微分方程为
由题已给定的滑块B的运动方程,可通过微分求得
AB杆受拉力。
AB杆受压力。
例10-2
质量为m的质点带有电荷e,以速度v0进入强度按E = Acoskt变化的均匀电场中,初速度方向与电场强度垂直,如图10-3所示。
质点在电场中受力![]() 作用。已知常数A,k,忽略质点的重力,试求质点的运动轨迹。
作用。已知常数A,k,忽略质点的重力,试求质点的运动轨迹。
图10-3
解:
该问题属于动力学第二类基本问题。取质点的初
始位置O为原点,建立坐标系如图所示。
质点的运动微分方程在x轴和y轴上的投影式分
别为
按题意,质点运动的初始条件为:当t = 0 时
vx = v0 ,vy = 0,x = y = 0
于是,运动微分方程(a)的定积分为
得质点速度为
(b)的定积分为
得质点运动方程为
从质点运动方程(c)中消去时间t,得到轨迹方程
轨迹为余弦曲线,如图所示。
例10-3
一圆锥摆,如图10-4所示。质量m = 0.1kg的小球系于长l = 0.3m的绳上,绳的另一端系在固定点O,并与铅直线成![]() 角。如小球在水平面内作匀速圆周运动,求小球的速度v与绳的张力F的大小。
角。如小球在水平面内作匀速圆周运动,求小球的速度v与绳的张力F的大小。
图10-4
解:
该问题属于动力学第一类基本问题与动力学第二类基本问题的混合问题。以小球为研究的质点。作用在质点上的力有重力mg和绳的拉力F。
质点运动微分方程在自然轴上的投影式为
绳的张力与拉力F的大小相等。
此例表明,向自然轴投影可以使动力学两类问题放开求解。
例10-4
粉碎机滚筒半径为R,绕通过中心的水平轴匀速转动,筒内铁球由筒壁上的凸棱带着上升。为了使铁球获得粉碎矿石的能量,铁球应在![]() 时(如图10-5所示)才掉下来。求滚筒每分钟的转数n。
时(如图10-5所示)才掉下来。求滚筒每分钟的转数n。
图10-5
解:
视铁球为质点。铁球在上升过程中,受到重力mg和筒壁的法向约束力FN、切向约束力F的作用。
质点运动微分方程在主法线上的投影式
铁球在未离开筒壁前的速度等于筒壁的速度,即
于是解得