QAQ：
A. ConneR and the A.R.C. Markland-N
题意：
有一个n层的楼，输入k个被封闭的楼层，有个人在第s层，问这个最少走多少步能找到一个不被封锁的楼层
思路：
暴力枚举即可。
代码：
#include <bits/stdc++.h> using namespace std; set<int> s; void solve(int n,int now,int k) { int ans = 0; while(1) { if(s.find(max(now-ans,1))==s.end()||s.find(min(n,now+ans))==s.end()) { break; } ++ans; // cout << now - ans << " " << now+ans << endl; } cout << ans << " "; } int main() { int t; cin >> t; while(t--) { s.clear(); int n,now,k; cin >> n >> now >> k; int x; while(k--) { cin >> x; s.insert(x); } solve(n,now,k); } return 0; }
B. JOE is on TV!
题意：
一个人去参加电视问答节目，假设他能答对所有题目，这个节目所能获得的奖金是每一轮奖金的累加和，而每一轮获得的奖金是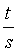
(s为这一轮开始的时的人数，t为这一轮淘汰的人数)，输入节目起始的参加人数n，求这个人最多能获得多少奖金。
思路：
答案是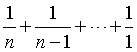
简易的证明如下，我们假设某一轮起始人数为s，这一轮淘汰了t个人，那么他对答案的贡献要明显小于我们上面的取值，因为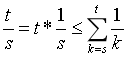
代码：
#include <bits/stdc++.h> using namespace std; int main() { double n; cin >> n; double ans = 1; for(int i = 2;i<=n;++i) ans+=(double(1.0)/double(i)); cout << ans << " "; return 0; }
C. NEKO's Maze Game
题意：
给你一个2*n的矩阵，有m次询问，每次询问输入一个点，假如这个点是可以经过的，那就堵住，反之，这个点就是更改为可以经过，对于每次查询，问能不能从（1，1）走到（2，n）
思路：
不能的走到的情况事实上只需要两个点就可以，一共是三种情况分别是，斜着两种以及竖着一种，我们可以对于输入的点进行分类讨论，假如这个点时由可经过变成不可经过，我们就查询对于该点来说的可能导致整条路不同的三个位置是否也堵住了，假如堵住了就将这两个点组成一个二元对用集合存储起来，假如这个点是由不可经过变成可经过的，同样查询上面三个位置，假如也堵住了，则需要从集合中删除这两个点构成的二元对。最后只要查询下集合是否为空即可。
代码：
#include <bits/stdc++.h> using namespace std; struct Point { int x,y; Point(int _x=0,int _y=0):x(_x),y(_y) {} bool operator<(const Point&b)const { if(x==b.x) return y<b.y; return x<b.x; } }; set<Point> s; set<pair<Point,Point> > s1; void op(Point&a,Point&b,int x) { if(x==1) { if(s.find(a)!=s.end()) { s1.insert(make_pair(a,b)); s1.insert(make_pair(b,a)); } } else { set<pair<Point,Point> >::iterator it1; it1 = s1.find(make_pair(a,b)); if(it1!=s1.end()) s1.erase(it1); it1 = s1.find(make_pair(b,a)); if(it1!=s1.end()) s1.erase(it1); } return ; } int main() { int n,p,r,c; Point tmp,temp; cin >> n >>p; //bool flag = false; while(p--) { cin >> tmp.x>>tmp.y; if(s.find(tmp)==s.end()) { s.insert(tmp); if(tmp.x==1) { temp = Point(2,tmp.y); op(temp,tmp,1); if(tmp.y>1) { temp = Point(2,tmp.y-1); op(temp,tmp,1); } if(tmp.y<n) { temp = Point(2,tmp.y+1); op(temp,tmp,1); } } else { temp = Point(1,tmp.y); op(temp,tmp,1); if(tmp.y>1) { temp = Point(1,tmp.y-1); op(temp,tmp,1); } if(tmp.y<n) { temp = Point(1,tmp.y+1); op(temp,tmp,1); } } } else { set<Point>::iterator it = s.find(tmp); s.erase(it); if(tmp.x==1) { temp = Point(2,tmp.y); op(temp,tmp,2); if(tmp.y>1) { temp = Point(2,tmp.y-1); op(temp,tmp,2); } if(tmp.y<n) { temp = Point(2,tmp.y+1); op(temp,tmp,2); } } else { temp = Point(1,tmp.y); op(temp,tmp,2); if(tmp.y>1) { temp = Point(1,tmp.y-1); op(temp,tmp,2); } if(tmp.y<n) { temp = Point(1,tmp.y+1); op(temp,tmp,2); } } } if(s1.empty()) printf("YES "); else printf("NO "); } return 0; }
D. Aroma's Search
题意：
二维平面上有若干个点，第i个点的坐标(xi,yi)满足xi=x_i-1*ax+bx,yi=y_y-1*ay+by
已知 ax,bx,ay,by,x0,y0 以及初始位置(xs,ys)
每秒钟可以往上下左右走1个单位
问在t秒内最多可以走到多少个点
思路：
数据范围很大，但观察下ax，ay都大于2，因此点的位置是呈现指数级递增的，因此可以先把点打出来。考虑点集是一个连续的区间，能走到的点的集合可以认为是处于两个点之间，我们去枚举作为端点的两个点l,r，那么总时间的花费就是dis(l,r)+min(dis(sta,l),dis(sta,r)，sta为起始位置，总获得的点数就是r-l+1。
代码：
#include<bits/stdc++.h> using namespace std; typedef long long ll; vector<ll> x,y; int main() { ll x0,y0,ax,ay,bx,by,xs,ys,t; cin >> x0 >> y0 >> ax >>ay >>bx >> by >> xs >> ys >> t; ll LIMIT = (ll)1e16<<1; for(ll a = x0,b = y0;a<=LIMIT&&b<=LIMIT;a = ax*a+bx,b =ay*b+by ) x.push_back(a),y.push_back(b); ll ans = 0; int len = x.size(); //cout << len << endl; for(int i = 0;i<len;i++) { for(int j = i ;j<len;j++) { ll tmp = abs(x[i]-x[j])+abs(y[i]-y[j]); if(min(abs(xs-x[i])+abs(ys-y[i]),abs(xs-x[j])+abs(ys-y[j]))<=t-tmp) ans = max(ans,(ll)j-i+1);//cout << x[i] << y[i] << " " << x[j] << " " << y[j] << endl ; } } cout << ans << " "; return 0; }