题意
|
Language: Connected Graph
Description An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices. For example,there are 4 different connected undirected graphs with 3 vertices. 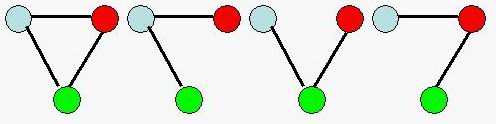 Input The input contains several test cases. Each test case contains an integer n, denoting the number of vertices. You may assume that 1<=n<=50. The last test case is followed by one zero. Output For each test case output the answer on a single line. Sample Input 1 2 3 4 0 Sample Output 1 1 4 38 Source |
给定n个点,每两个点间至多连一条无向边,问任意连边,这些点能够成的无向连通图的个数
分析
参照ustcscuwf的题解。
典型的递推,裸算几乎不可能,生成树图的个数都要通过母函数进行推导和计算,这个更加复杂,递推公式为F(n)=sigma(F(n-k)F(k)C(n-2,k-1)*(2^k-1))。显然要用大数计算,最后的数字有三百多位。
这个递推还是比较好理解的,就是分成两个子连通部分,要想整个连通,那么两个子连通图中间必然要有一条边连接,在划分子连通时,注意固定子连通中的各一个点,防止重复计数。规定连边必须向固定的点(i)连边。
时间复杂度(O(n^2 S^2))
代码
#include<iostream>
#include<cstring>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0,w=1;rg char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') w=-1;ch=getchar();}
while(isdigit(ch)) data=data*10+ch-'0',ch=getchar();
return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;
co int N=60,S=600;
int n;
struct A{
int a[S],len;
il A operator/(co int x)co{
A ans;
memset(ans.a,0,sizeof ans.a);
ans.len=0;
int num=0;
for(int i=len;i;--i){
num=num*10+a[i];
ans.a[i]=num/x;
num%=x;
if(!ans.len&&ans.a[i]) ans.len=i;
}
return ans;
}
il A operator+(co A&x)co{
A ans;
memset(ans.a,0,sizeof ans.a);
for(int i=1;i<=max(len,x.len);++i){
ans.a[i]+=a[i]+x.a[i];
ans.a[i+1]=ans.a[i]/10;
ans.a[i]%=10;
}
ans.len=max(len,x.len);
if(ans.a[ans.len+1]) ++ans.len;
return ans;
}
il A operator*(co A&x)co{
A ans;
memset(ans.a,0,sizeof ans.a);
for(int i=1;i<=len;++i)
for(int j=1;j<=x.len;++j){
ans.a[i+j-1]+=a[i]*x.a[j];
ans.a[i+j]+=ans.a[i+j-1]/10;
ans.a[i+j-1]%=10;
}
ans.len=len+x.len-1;
if(ans.a[ans.len+1]) ++ans.len;
return ans;
}
}f[N],p[N];
il A C(int x,int y){
A ans;
ans.len=ans.a[1]=1;
for(int i=y,j=1;j<=x;--i,++j){
int t=i;
A tmp;
tmp.len=0;
while(t){
tmp.a[++tmp.len]=t%10;
t/=10;
}
ans=ans*tmp/j;
}
return ans;
}
il void print(co A&x){
for(int i=x.len;i;--i) printf("%d",x.a[i]);
puts("");
}
int main(){
for(int i=1;i<=50;++i){
ll t=(1LL<<i)-1;
while(t){
p[i].a[++p[i].len]=t%10;
t/=10;
}
}
f[1].len=f[2].len=f[1].a[1]=f[2].a[1]=1;
for(int i=3;i<=50;++i)
for(int j=1;j<=i-1;++j)
f[i]=f[i]+C(j-1,i-2)*f[j]*f[i-j]*p[j];
while(read(n)) print(f[n]);
return 0;
}