https://www.bilibili.com/video/av18512769?t=1874
第二题: 给定一个正整数s, 判断一个数组arr中,是否有一组数字加起来等于s。
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int a[100];
int subset[100][100];
int rec_subset(int i,int s) // 递归
{
if (s == 0)
return 1;
else if (i == 0)
return a[0] == s;
else if (a[i] > s)
return rec_subset(i - 1, s);
else
{
int A = rec_subset(i - 1, s - a[i]);
int B = rec_subset(i - 1, s);
return A || B;
}
}
int dp_subset(int lon, int S) // 动态规划
{
for (int i = 0; i < lon; i++) // 递归出口
{
subset[i][0] = 1;
}
for (int i = 0; i <= S; i++) // 递归出口
{
subset[0][i] = 0;
}
subset[0][a[0]] = 1, subset[0][0] = 1;
for (int i = 1; i < lon; i++)
{
for (int j = 1; j <= S; j++)
{
if (a[i] > j) // 递归出口
subset[i][j] = subset[i - 1][j];
else
{
int A = subset[i - 1][j - a[i]];
int B = subset[i - 1][j];
subset[i][j] = A || B;
}
}
}
return subset[lon - 1][S];
}
int main(void)
{
int lon, S;
while (scanf("%d%d", &lon, &S) != EOF)
{
for (int i = 0; i < lon; i++)
{
scanf("%d", &a[i]);
}
printf("%d
", rec_subset(lon - 1, S));
printf("%d
", dp_subset(lon, S));
}
system("pause");
return 0;
}
/*测试数据
6 9
3 34 4 12 5 2
6 13
3 34 4 12 5 2
*/
这道题依旧是利用选与不选,不过要兵分两路判断是否存在。
递归出口:
① 当已经选中的元素的和 == s 时, 返回 存在
② 当只有一个元素时,如果 a[0] == s 返回存在
如果 a[0] != s 返回不存在
③ 当 当前元素比 s 大时,直接走不选 那条路 (这样可以起到剪枝的作用)
函数关系 :
选 : 个数减一,s - a[i]
不选 : 个数减一,s 不变
两条路只要一条路成功,就成功
状态数组 :
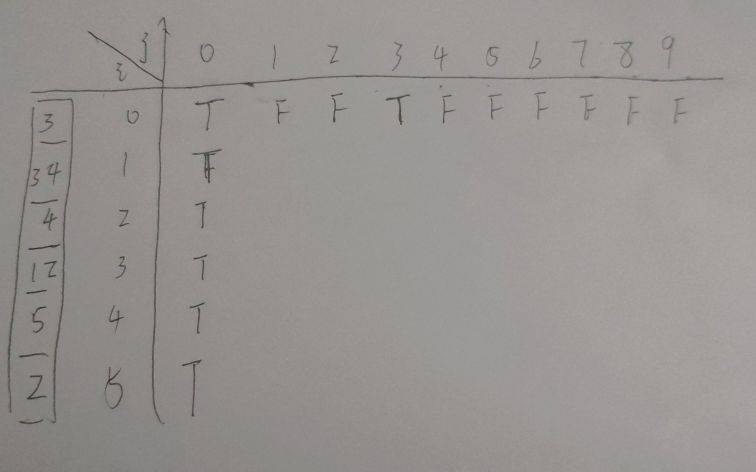
这是初始化后的数组,需要注意的两点时,(0,0)为 true,(0,a[0])为true
然后根据递推关系就可以推出完整的状态数组。
个人感悟:
1,关于递归出口:else if (a[i] > s)
return rec_subset(i - 1, s);
我想了一下,在递归中把这句去掉也是没有问题,反而去掉之后还可以用于数组元素存在负数的时候,
不过,既然已经说皆为正数,判断一下可以省下递归次数
而在 dp 中:if (a[i] > j) // 递归出口
subset[i][j] = subset[i - 1][j];
这个就必须要有了,不然你只能再造一个下标为负数时所对应的数组。
不过,还是有点疑惑,我用 VS 调试时,下标为负数却没有报错,不知道为什么
2,关于 rec 与 dp 一些看法
① 刚学习算法不久,一直觉得想出递归这种函数的人是真的秀。
递归是你想拿到某样东西,你就要相信你前面的人可以为你铺路,让你可以拿到你想要的。
As far as I'm concerned,递归是从后面找到前面,再从前面递推到后面,而它也正是利用这种递推关系找到所需要的初始条件,再从初始条件递推回去。
② 而动态规划呢,是用数组去储存递归时的状态,或用一维或用二维,
递归需要找到初始条件,而 dp 不用找,是直接对初始条件进行赋值,
而这里需要用到二维数组的原因,应该就是,每一个 j (即其所对对应 a[j] ) 存在多种状态下的 s,所以还要再加一维
3,之后才学了 DFS 才知道这题也可以用 DFS 求解
========== ========= ======== ======= ====== ===== ==== === == =
忆秦娥 · 娄山关 毛润之
西风烈, 长空雁叫霜晨月。
霜晨月, 马蹄声碎, 喇叭声咽。
雄关漫道真如铁,而今迈步从头越。
从头越,苍山如海,残阳如血。