有理有据的结论题
Problem Description
"The Werewolves" is a popular card game among young people.In the basic game, there are 2 different groups: the werewolves and the villagers.
Each player will debate a player they think is a werewolf or not.
Their words are like "Player x is a werewolf." or "Player x is a villager.".
What we know is :
1. Villager won't lie.
2. Werewolf may lie.
Of cause we only consider those situations which obey the two rules above.
It is guaranteed that input data exist at least one situation which obey the two rules above.
Now we can judge every player into 3 types :
1. A player which can only be villager among all situations,
2. A player which can only be werewolf among all situations.
3. A player which can be villager among some situations, while can be werewolf in others situations.
You just need to print out the number of type-1 players and the number of type-2 players.
No player will talk about himself.
Each player will debate a player they think is a werewolf or not.
Their words are like "Player x is a werewolf." or "Player x is a villager.".
What we know is :
1. Villager won't lie.
2. Werewolf may lie.
Of cause we only consider those situations which obey the two rules above.
It is guaranteed that input data exist at least one situation which obey the two rules above.
Now we can judge every player into 3 types :
1. A player which can only be villager among all situations,
2. A player which can only be werewolf among all situations.
3. A player which can be villager among some situations, while can be werewolf in others situations.
You just need to print out the number of type-1 players and the number of type-2 players.
No player will talk about himself.
Input
The first line of the input gives the number of test cases T.Then T test cases follow.
The first line of each test case contains an integer N,indicating the number of players.
Then follows N lines,i-th line contains an integer x and a string S,indicating the i-th players tell you,"Player x is a S."
The first line of each test case contains an integer N,indicating the number of players.
Then follows N lines,i-th line contains an integer x and a string S,indicating the i-th players tell you,"Player x is a S."
limits:
1≤T≤10
1≤N≤100,000
1≤x≤N
S∈ {"villager"."werewolf"}
1≤T≤10
1≤N≤100,000
1≤x≤N
S∈ {"villager"."werewolf"}
Output
For each test case,print the number of type-1 players and the number of type-2 players in one line, separated by white space.
Sample Input
1
2
2 werewolf
1 werewolf
Sample Output
0 0
题目大意
现在有N个人，每个人要么是第一类：说的全是真话；要么是第二类：说的可能是假话。
每一个人x都指认另一个人y是第一类或第二类人。
请问在所有合法的情况下，有多少人必定是第一类人、有多少人必定是第二类人？
题目分析
为什么好多人第一眼看去2-sat？为什么有些人（MikuKnight）以为这真的是把狼人杀？？？
以上吐槽结束。题意已经大概写了一下了。
暴力想法
暴力做法的第一反应肯定是爆搜。
时间复杂度O(2^n)
推点性质
再一眼看去：诶这题意有点意思啊，为什么问的是“所有合法”情况下？
转念一想，那么如果每个人都说假话不也合法吗？
于是得到了这题的第一个性质：每一个人都可能是第二类人。
既然如此，只需要判断一个人能不能够成为第一类人就行了。
方法很简单，对于每一个人，假定他说真话合法，于是dfs下去检查是否矛盾。细节在于铁定说假话的人的话是没有后继效用的，意即他指认的第一类人并不一定合法。
时间复杂度O(n^2)
再推点性质
打多校时候同队的ZXB机智地猜了一条结论（以下简称“一定是第二类人的人”为“铁狼”）：
结论的充分性是显然的，考虑其必要性。
首先一个人是铁狼的充要条件是其不可能成为第一类人。由上面的性质可以得到，问题的补集就变成是：哪些人不能成为第二类人。
由于每一个人会且只会指认一个人，最基础的判定方法自然是上一条中的dfs。
考虑指认关系形成的图中环的部分。若环中有超过一条“werewolf”边，在合法情况下，被指认人的判定可以是被信任的也可以是不被信任的；再者，由于问题询问的是“所有合法情况”，被指认人的后继因此也可以被信任或不被信任。换句话说，一旦被指认，他之后的所有后继都形同虚设、模棱两可。
再考虑图中非环部分。由于每个人都可能是第二类人，于是只需考虑第一类边。自然，非法情况当且仅当（直接或间接）指认铁狼为村民。
这样，就证明了性质的充要性。
可能会犯的错误1
把边(u,v,werewolf)的v的后继全部删去。
这个情况在环上成立然而链上不成立。
可能会犯的错误2
某些方法会出现的找环时候的错误。
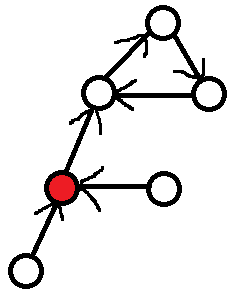
挂张图，这个就不细说了我错在这里没发现好久，属于做题的经验，还是多积累吧。
后记
话说在这题上和法老拉平还是有点小激动啊
1 #include<cstdio> 2 #include<cctype> 3 #include<cstring> 4 const int maxn = 100035; 5 6 struct Edge 7 { 8 int y,opt; 9 }edges[maxn]; 10 int T,n,ans; 11 char ch[13]; 12 int vis[maxn],deg[maxn],sv[maxn],cnt,tag; 13 int head[maxn],nxt[maxn]; 14 int qead[maxn],qxt[maxn],qdges[maxn],edgeTot; 15 bool done[maxn]; 16 17 int read() 18 { 19 char ch = getchar(); 20 int num = 0; 21 bool fl = 0; 22 for (; !isdigit(ch); ch = getchar()) 23 if (ch=='-') fl = 1; 24 for (; isdigit(ch); ch = getchar()) 25 num = (num<<1)+(num<<3)+ch-48; 26 if (fl) num = -num; 27 return num; 28 } 29 void addedge(int u, int v) 30 { 31 qdges[++edgeTot] = v, qxt[edgeTot] = qead[u], qead[u] = edgeTot; 32 } 33 void dfs(int x) 34 { 35 vis[x] = 1; 36 for (int i=head[x]; i!=-1; i=nxt[i]) 37 { 38 int v = edges[i].y; 39 if (vis[v]){ 40 if (vis[v]==1) vis[v] = 2, sv[++sv[0]] = v; 41 vis[x] = 2; 42 return; 43 } 44 dfs(v); 45 if (vis[v]==2) vis[x] = 2; 46 } 47 } 48 void search(int x, int top, int tot) 49 { 50 for (int i=head[x]; i!=-1; i=nxt[i]) 51 { 52 int v = edges[i].y, cnt = tot; 53 if (!edges[i].opt){ 54 if (cnt){ 55 tag = -1; 56 return; 57 } 58 cnt = 1, tag = v; 59 } 60 if (v==top) return; 61 search(v, top, cnt); 62 } 63 } 64 void wit(int x) 65 { 66 if (done[x]) return; 67 done[x] = 1; 68 for (int i=qead[x]; i!=-1; i=qxt[i]) 69 wit(qdges[i];); 70 } 71 int main() 72 { 73 // freopen("1009.in","r",stdin); 74 // freopen("1009.out","w",stdout); 75 T = read(); 76 while (T--) 77 { 78 memset(head, -1, sizeof head); 79 memset(qead, -1, sizeof qead); 80 memset(done, 0, sizeof done); 81 memset(vis, 0, sizeof vis); 82 memset(deg, 0, sizeof deg); 83 memset(vv, 0, sizeof vv); 84 n = read(), edgeTot = sv[0] = ans = 0; 85 for (int i=1; i<=n; i++) 86 { 87 edges[i].y = read(), scanf("%s",ch); 88 edges[i].opt = ch[0]=='v'; 89 nxt[i] = head[i], head[i] = i; 90 deg[edges[i].y]++; 91 if (edges[i].opt) addedge(edges[i].y, i); 92 } 93 for (int i=1; i<=n; i++) 94 if (!vis[i]&&!deg[i]) dfs(i); 95 for (int i=1; i<=n; i++) 96 if (!vis[i]) dfs(i); 97 for (int i=1; i<=sv[0]; i++) 98 { 99 cnt = 0, tag = -1; 100 search(sv[i], sv[i], 0); 101 if (tag==-1) continue; 102 wit(tag); 103 } 104 for (int i=1; i<=n; i++) 105 if (done[i]) ans++; 106 printf("0 %d ",ans); 107 } 108 return 0; 109 }
END