看似区间数据结构的一道题
题目描述
Bessie and her friends are playing a unique version of poker involving a deck with N (1 <= N <= 100,000) different ranks, conveniently numbered 1..N (a normal deck has N = 13). In this game, there is only one type of hand the cows can play: one may choose a card labeled i and a card labeled j and play one card of every value from i to j. This type of hand is called a "straight".
Bessie's hand currently holds a_i cards of rank i (0 <= a_i <= 100000). Help her find the minimum number of hands she must play to get rid of all her cards.
一个牛有N堆牌,每堆排数量不等。一只牛一次可以将第i张到第j张各打一张出去,问最少几次打完
容易想到将这n个数形象地看做一个山脉形状的图。问题就可以形象地理解为,求将一座「山脉」以类似俄罗斯方块的消除方式消除的最小次数。
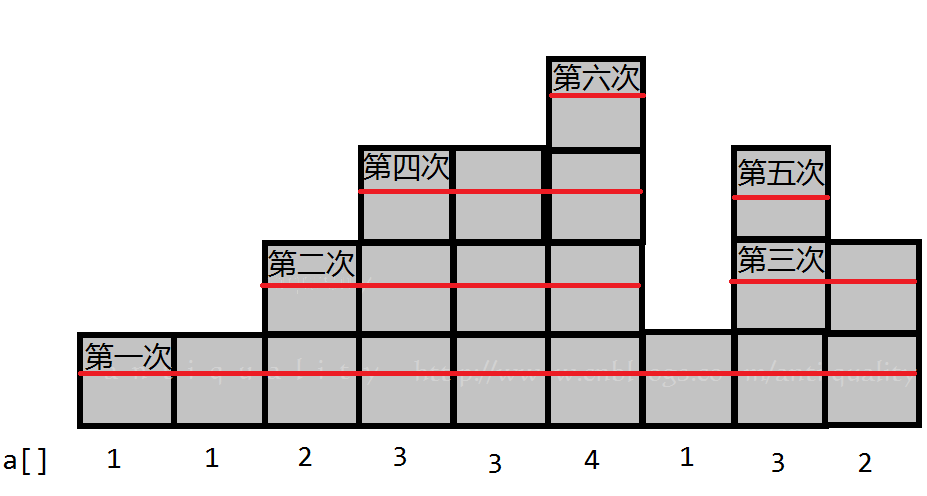
差不多就这样
自然地,就会想到用维护区间最小值的方法做这题。但是由于删除之后之前的区间内的最小值已经过气了,我们不得不1.修改区间内的数,都减去min值;2.维护区间第k小数……
显然都比较不可行(好像硬要数据结构上也是可行的但是这题luogu上被评为普及/提高-)。
我们发现逐个读入的时候,如果当前a[i] > a[i-1]那么必定要操作a[i] - a[i-1]次。另一方面当a[i] < a[i-1]时,由于消除操作可以区间进行,因为现在的值小于之前操作的,那么以前消除时候顺带延展到当前就行了。
这样一来结果第i次的决策就只跟a[i-1]有关,因此不必保存a[]数组。
以上,贪心即可。
(写这篇是因为想到以后学数据结构可能会学傻掉……所以来篇假数据结构提醒一下)