Delta-wave

Delta-wave

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4602    Accepted Submission(s): 1745

Problem Description

A triangle field is numbered with successive integers in the way shown on the picture below.



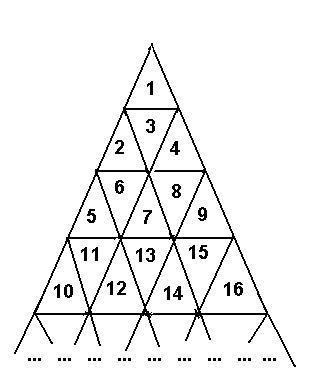
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.

Write the program to determine the length of the shortest route connecting cells with numbers N and M.

 

Input

Input contains two integer numbers M and N in the range from 1 to 1000000000 separated with space(s).

 

Output

Output should contain the length of the shortest route.

 

Sample Input

6 12

 

Sample Output

3

 

思路：数学题，把每个数字对应的行号（1，2，3。。。。。）算出来，行号h = sqrt（n）为整数则不加1，否则加1，得到的就是行号，再分别算出从左边和从右边起的列号（1，2，3。。。），右列号rl = (h*h-n)/2+1，左列号ll = (n-((h-1)*(h-1)+1))/2+1，然后两个数对应的行，列号相减的绝对值之和就是最短路线。

 

 

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main()
{
    int n,m,h_n,h_m,ll_n,rl_n,rl_m,ll_m,r;
    while(~scanf("%d%d",&n,&m))
    {
        if(sqrt(n)>(int)sqrt(n))
           h_n = (int)sqrt(n)+1;
        else
           h_n = (int)sqrt(n);
        rl_n = (h_n*h_n-n)/2+1;
        ll_n = (n-((h_n-1)*(h_n-1)+1))/2+1;
         if(sqrt(m)>(int)sqrt(m))
           h_m = (int)sqrt(m)+1;
        else
           h_m = (int)sqrt(m);
        rl_m = (h_m*h_m-m)/2+1;
        ll_m = (m-((h_m-1)*(h_m-1)+1))/2+1;
        r = abs(h_n-h_m)+abs(ll_n-ll_m)+abs(rl_n-rl_m);
        printf("%d ",r);
    }
    return 0;
}