l 树:满足以下条件:
有且仅有一个根节点。
当节点数大于1时,除根节点为其余节点可以划分为m个互不相交的有限集,其中每一个集合本身又是一棵树,称为子树。
l 概念
- Node结点
- Degree结点的度
- Leaf 叶子结点
- 分支结点
- 孩子结点child
- 父节点
- 兄弟节点
- 树的度
- 结点的层次
- 树的高度
- 森林
- 有序树和无序树
- 二叉树
- 二叉树是有序树
定义:
- 二叉树有且仅有一个根结点
- 结点数大于一时,每个结点最多有两个子树。
- 二叉树的子树有左右之分,且其次序不能颠倒
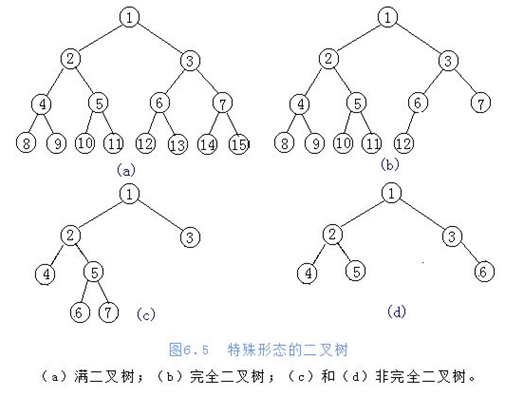
性质
- 二叉树第i层之多有2i-1 个节点(i>.=1);
- 深度为k的二叉树之多有2k-1个结点。
- 对于任意一棵二叉树来说,如果其叶子结点数n0 度为2 的结点数为n2则n0=n2+1
- 满二叉树:一棵深度为k且有2k-1个结点的二叉树称为满二叉树。
-
- 完全二叉树:深度为K 有n个结点的二叉树,当且仅当每一个结点都与深度为k的满二叉树中编号为1·~n的结点一一对应时,称作完全二叉树。
特点:
- 叶子结点只可能在层次最大的两层出现
- 对于任意一结点,若其右分支下子孙最大层次为P,则其左分支最大层次必P或者P+1
- N个结点的完全二叉树深度为【log2n】+1 (【】:取整)
- 对于n个结点的二叉树,如果按照层次编号,对于任意一结点,I E(1,n)
- I>1 ,父节点【i/2】
- 2i>n , 无左孩子,2i<=n 其左孩子是2i
- 2i+1>n 无右孩子,否则右孩子是2i+1