1 问题描述
给定一个有向图,求取此图的拓扑排序序列。
那么,何为拓扑排序?
定义:将有向图中的顶点以线性方式进行排序。即对于任何连接自顶点u到顶点v的有向边uv,在最后的排序结果中,顶点u总是在顶点v的前面。
2 解决方案
2.1 基于减治法实现
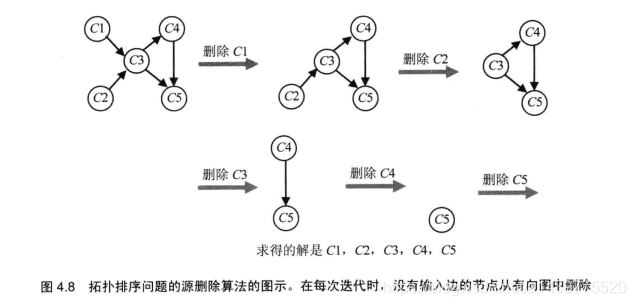
实现原理:不断地做这样一件事,在余下的有向图中求取一个源(source)(PS:定义入度为0的顶点为有向图的源),它是一个没有输入边的顶点,然后把它和所有从它出发的边都删除。(如果有多个这样的源,可以任意选择一个。如果这样的源不存在,算法停止,此时该问题无解),下面给出《算法设计与分析基础》第三版上一个配图:
package com.liuzhen.chapterFour;
import java.util.Stack;
public class TopologicalSorting {
//方法1:基于减治法:寻找图中入度为0的顶点作为即将遍历的顶点,遍历完后,将此顶点从图中删除
/*
* 参数adjMatrix:给出图的邻接矩阵值
* 参数source:给出图的每个顶点的入度值
* 该函数功能:返回给出图的拓扑排序序列
*/
public char[] getSourceSort(int[][] adjMatrix,int[] source){
int len = source.length; //给出图的顶点个数
char[] result = new char[len]; //定义最终返回路径字符数组
int count = 0; //用于计算当前遍历的顶点个数
boolean judge = true;
while(judge){
for(int i = 0;i < source.length;i++){
if(source[i] == 0){ //当第i个顶点入度为0时,遍历该顶点
result[count++] = (char) ('a'+i);
source[i] = -1; //代表第i个顶点已被遍历
for(int j = 0;j < adjMatrix[0].length;j++){ //寻找第i个顶点的出度顶点
if(adjMatrix[i][j] == 1)
source[j] -= 1; //第j个顶点的入度减1
}
}
}
if(count == len)
judge = false;
}
return result;
}
/*
* 参数adjMatrix:给出图的邻接矩阵值
* 函数功能:返回给出图每个顶点的入度值
*/
public int[] getSource(int[][] adjMatrix){
int len = adjMatrix[0].length;
int[] source = new int[len];
for(int i = 0;i < len;i++){
//若邻接矩阵中第i列含有m个1,则在该列的节点就包含m个入度,即source[i] = m
int count = 0;
for(int j = 0;j < len;j++){
if(adjMatrix[j][i] == 1)
count++;
}
source[i] = count;
}
return source;
}
public static void main(String[] args){
TopologicalSorting test = new TopologicalSorting();
int[][] adjMatrix = {{0,0,1,0,0},{0,0,1,0,0},{0,0,0,1,1},{0,0,0,0,1},{0,0,0,0,0}};
int[] source = test.getSource(adjMatrix);
System.out.println("给出图的所有节点(按照字母顺序排列)的入度值:");
for(int i = 0;i < source.length;i++)
System.out.print(source[i]+" ");
System.out.println();
char[] result = test.getSourceSort(adjMatrix, source);
System.out.println("给出图的拓扑排序结果:");
for(int i = 0;i < result.length;i++)
System.out.print(result[i]+" ");
}
}
运行结果:
给出图的所有节点(按照字母顺序排列)的入度值:
0 0 2 1 2
给出图的拓扑排序结果:
a b c d e
2.2 基于深度优先查找实现
引用自网友博客中一段解释:
除了使用上面2.1中所示算法之外,还能够借助深度优先遍历来实现拓扑排序。这个时候需要使用到栈结构来记录拓扑排序的结果。
同样摘录一段维基百科上的伪码:
L ← Empty list that will contain the sorted nodes
S ← Set of all nodes with no outgoing edges
for each node n in S do
visit(n)
function visit(node n)
if n has not been visited yet then
mark n as visited
for each node m with an edgefrom m to ndo
visit(m)
add n to L
DFS的实现更加简单直观,使用递归实现。利用DFS实现拓扑排序,实际上只需要添加一行代码,即上面伪码中的最后一行:add n to L。
需要注意的是,将顶点添加到结果List中的时机是在visit方法即将退出之时。
此处重点在于理解:上面伪码中的最后一行:add n to L,对于这一行的理解重点在于对于递归算法执行顺序的理解,递归执行顺序的核心包括两点:1.先执行递归,后进行回溯;2.遵循栈的特性,先进后出。此处可以参考本人另外一篇博客:递归执行顺序的探讨
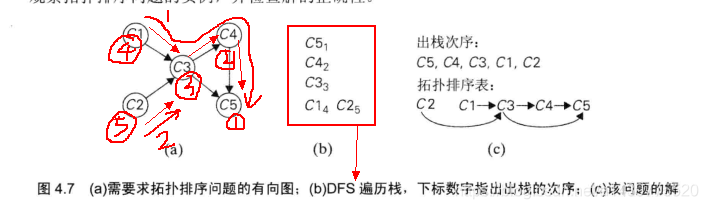
下面请看一个出自《算法设计与分析基础》第三版上一个配图:
package com.liuzhen.chapterFour;
import java.util.Stack;
public class TopologicalSorting {
//方法2:基于深度优先查找发(DFS)获取拓扑排序
public int count1 = 0;
public Stack<Character> result1;
/*
* adjMatrix是待遍历图的邻接矩阵
* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历
*/
public void dfs(int[][] adjMatrix,int[] value){
result1 = new Stack<Character>();
for(int i = 0;i < value.length;i++){
if(value[i] == 0)
dfsVisit(adjMatrix,value,i);
}
}
/*
* adjMatrix是待遍历图的邻接矩阵
* value是待遍历图顶点用于是否被遍历的判断依据,0代表未遍历,非0代表已被遍历
* number是当前正在遍历的顶点在邻接矩阵中的数组下标编号
*/
public void dfsVisit(int[][] adjMatrix,int[] value,int number){
value[number] = ++count1; //把++count1赋值给当前正在遍历顶点判断值数组元素,变为非0,代表已被遍历
for(int i = 0;i < value.length;i++){
if(adjMatrix[number][i] == 1 && value[i] == 0) //当,当前顶点的相邻有相邻顶点可行走且其为被遍历
dfsVisit(adjMatrix,value,i); //执行递归,行走第i个顶点
}
char temp = (char) ('a' + number);
result1.push(temp);
}
public static void main(String[] args){
TopologicalSorting test = new TopologicalSorting();
int[][] adjMatrix = {{0,0,1,0,0},{0,0,1,0,0},{0,0,0,1,1},{0,0,0,0,1},{0,0,0,0,0}};
int[] value = new int[5];
test.dfs(adjMatrix, value);
System.out.println();
System.out.println("使用DFS方法得到拓扑排序序列的逆序:");
System.out.println(test.result1);
System.out.println("使用DFS方法得到拓扑排序序列:");
while(!test.result1.empty())
System.out.print(test.result1.pop()+" ");
}
}
运行结果:
使用DFS方法得到拓扑排序序列的逆序:
[e, d, c, a, b]
使用DFS方法得到拓扑排序序列:
b a c d e