2021.2.6 刷题（对称二叉树、相同二叉树）

1.对称二叉树
题目链接：https://leetcode-cn.com/problems/symmetric-tree/
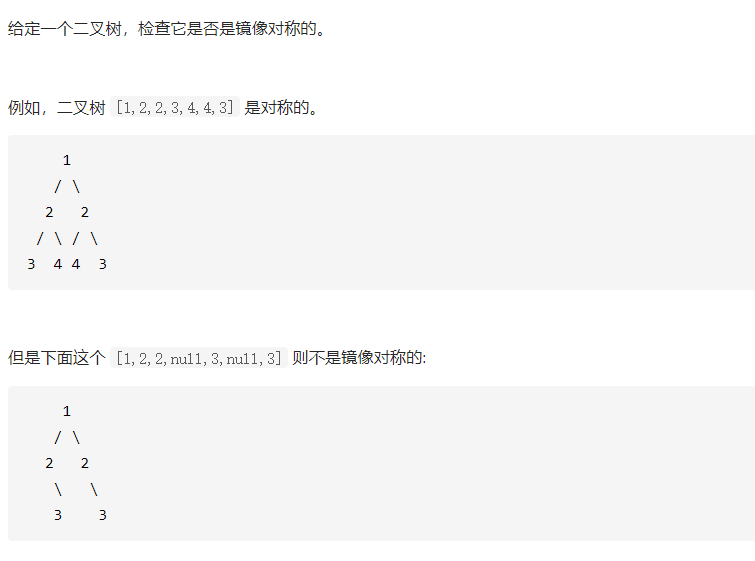
题目描述：

题解：

class Solution {
public:
    bool check(TreeNode *p, TreeNode *q) {
        if (p == NULL && q == NULL) return true;  
        if (p == NULL ) return false;             
        if (q == NULL) return false;
        if (p->val != q->val)
            return false;
        else
            return check(p->left, q->right) && check(p->right, q->left);
    }

    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};

2.相同的树
题目链接：https://leetcode-cn.com/problems/same-tree/
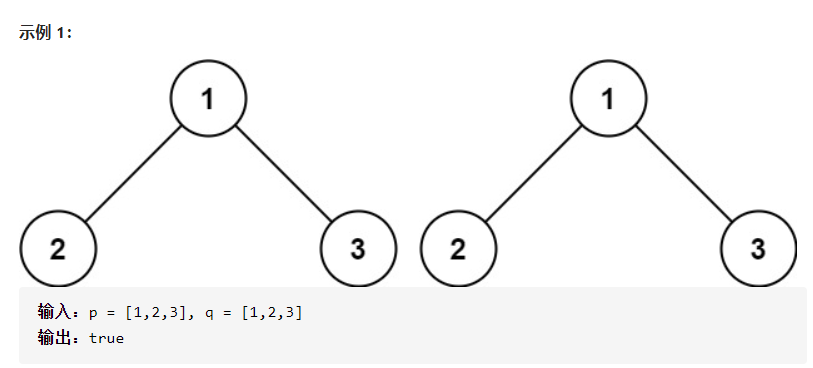
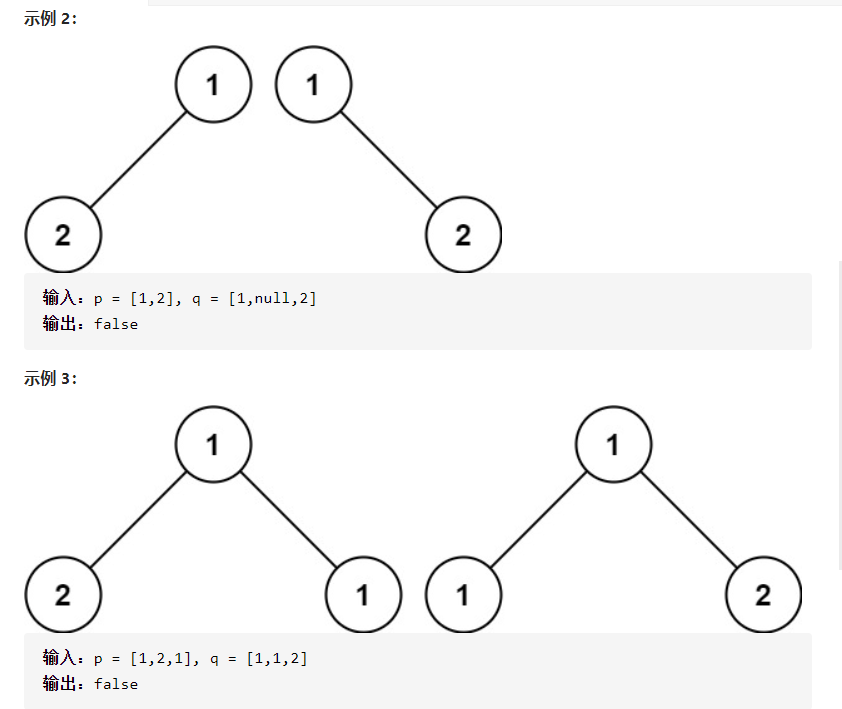
题目描述：给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

题解：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    
    bool isSameTree(TreeNode* p, TreeNode* q) {
         //排查空节点情况
        if(p == nullptr && q != nullptr)
            return false;
        else if(p != nullptr && q == nullptr)
            return false;
        else if(p == nullptr && q == nullptr)
            return true;
        //排查节点值不相同的情况
        else if (p->val != q->val) 
            return false;
        bool left = isSameTree(p->left, q->left);
        bool right = isSameTree(p->right, q->right);
        return left && right;
    }
};

3.另一棵树的子树
题目链接：https://leetcode-cn.com/problems/subtree-of-another-tree
题目描述：
给定两个非空二叉树 s 和 t，检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。

题解：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* p, TreeNode* q)
    {
        if(!p && !q) return true;
        if(!p || !q) return false;
        return p->val == q->val && compare(p->left, q->left) && compare(p->right, q->right);
    }
    bool isSubtree(TreeNode* s, TreeNode* t) {
        if(!s) return false;
        if(compare(s, t)) return true;
        return isSubtree(s->left, t) || isSubtree(s->right, t);
    }
};