倍增
原理:
只递推状态空间在2的整数次幂位置上的值作为代表。当需要其他位置的值时,我们通过“任意整数可以表示成若干个2的次幂项的和”这一性质,使用之前求出的代表值拼出所需要的值。
要求:
状态空间关于2的次幂具有可划分性
一个例子:快速幂(体现倍增与二进制划分思想)
1 int power(int a,int b,int p) 2 { 3 int ans=1; 4 while(b) 5 { 6 if(b & 1)ans=ans*a%p;//取出最后一位,判断b是否为奇数 7 a=a*a%p;//每一位按二进制更新权值 8 b>>=1;//舍弃最后一位 9 } 10 return ans; 11 }
快速幂忘了,多花了十分钟重新学。。。我太弱了QAQ
P.S.位运算什么的自己去看看就好了,很有用的。
倍增实现ST算法(划重点)
先提一下,ST算法主要是用来解决区间最值问题的(RMQ)
RMQ:给定一个长度为N的数列A,求下标为闭区间[l,r]中Ai的最值。
ST算法复杂度:O(nlogn) 预处理,O(1)在线回答
实现:
设Fi,j表示子区间[i,i+2j-1]里的最大值,也就是从i开始的2j个数的最大值。边界F[i,0]=A[i]。
当询问任意区间[l,r]的最值时,先计算出区间长度,满足2k<r-l+1的前提下最大的k。
那么 从l开始的2k个数 与 以r结尾的2k个数 两端一定覆盖了l,r。
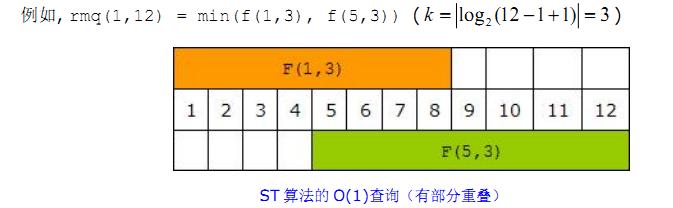
code:
1 int log[N];//log[i]表示log2 d向下取整 2 log[0]=-1;//边界条件,使log[1]=0; 3 void ST_prework() 4 { 5 for(int i=1;i<=n;i++) 6 f[i][0]=a[i],log[i]=log[i>>1]+1;//预处理边界,log值 7 for(int j=1;j<log[N];j++) //共能划分出log 2 N个区间 8 for(int i=1;i+(1<<j)-1<=n;i++) //当前区间要小于总区间长度 9 f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); 10 } 11 int ST_query(int l,int r) 12 { 13 int k=log[r-l+1]; //求k 14 return max(f[l][k],f[r-(1<<k)+1][k]); //两段取最大值 15 }
总的来说,ST表在RMQ问题上,不管是时间还是空间都表现得非常优秀。但是一遇到修改,ST表就不好维护了。
这时我们就要用到更加复杂高级的数据结构——线段树!
下篇更吧。线段树还不是很熟。QAQ