哈哈哈哈哈哈哈哈哈哈哈哈,终于把这道题补出来了_(:з」∠)_
来写题解啦。
_(:з」∠)_ _(:з」∠)_ _(:з」∠)_ _(:з」∠)_ _(:з」∠)_
哈哈哈哈哈哈,从9月16日打了这个题之后就一直在补这道题,今天终于a了,哈哈哈哈哈哈。
先把代码贴上,有时间再好好写题解,哈哈哈哈哈哈。ヾ(◍°∇°◍)ノ゙ヾ(◍°∇°◍)ノ゙ヾ(◍°∇°◍)ノ゙ヾ(◍°∇°◍)ノ゙ヾ(◍°∇°◍)ノ゙
代码,嘻嘻:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N=1e5+10; 5 const int mod=998244353; 6 ll qpow(ll x, int q){ 7 ll res = 1; 8 while(q){ 9 if(q%2) res = res*x%mod; 10 x = x*x%mod; 11 q /= 2; 12 } 13 return res; 14 } 15 int main(){ 16 int n,m; 17 ll ans; 18 while(~scanf("%d%d",&n,&m)){ 19 if(m>n)printf("0 "); 20 else if(n%2==1&&m%2==0||n%2==0&&m%2==1)printf("0 "); 21 else if(n==0&&m==0)printf("1 "); 22 else if(m==0){ 23 if(n%2==1)printf("0 "); 24 else if(n%2==0){ 25 if((n/2)%2==1)printf("998244352 "); 26 else printf("1 "); 27 } 28 } 29 else{ 30 ans=1; 31 for(int i=n-m+2;i<=n+m-2;i+=2) 32 ans=(ans*i)%mod; 33 ans=(ans*n)%mod; 34 ll temp=1; 35 for(int i=1;i<=m;i++) 36 temp=(i*temp)%mod; 37 ll cnt; 38 cnt=qpow(temp,mod-2); 39 //cout<<"aaaaaaaaaaaaaaaa"<<endl; 40 ans=ans*cnt%mod; 41 ans=((n-m)/2)%2==0?ans:-ans; 42 ans=(ans+mod)%mod; 43 printf("%lld ",ans%mod); 44 } 45 } 46 return 0; 47 }
溜啦溜啦,哈哈哈哈哈哈哈哈。
今天来写题解啦。
1000ms
Input Format
Multiple test cases (no more than 100).
Each test case contains one line consisting of two integers n and m.
1≤n≤109,0≤m≤104.
Output Format
Output the answer in a single line for each test case.
样例输入
2 0 2 1 2 2
样例输出
998244352 0 2
题目来源
题目一开始没看懂什么意思,后来知道是切比雪夫多项式后,才明白题目要求的是什么。
在多项式中求xm的系数。
切比雪夫多项式, 自行百度。
切比雪夫多项式的公式:
公式1:
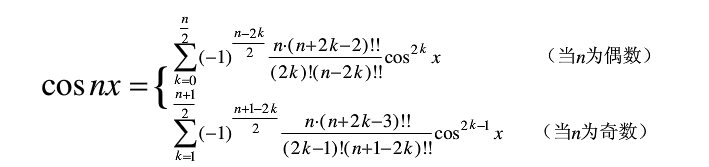
公式2:
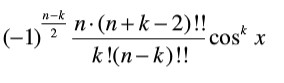
切比雪夫多项式举例:

我是用公式2写的代码。
通过研究这个公式,可以发现:
1.当n和m奇偶性不同的时候,公式结果为0;
2.当m为0的时候可以发现,结果是有规律的。1,0,-1,0,4个一循环,就可以判断if(n%2==1)结果为0,
if((n/2)%2==1),结果为-1,if((n/2)%2==0)结果为1;
3.因为只有n和m同奇或者同偶,用公式计算,通过分析公式2,可以将公式简化。n!!是二阶乘的意思,就是n*(n-2)*(n-4)*(n-6)*...2;
可以将公式上下抵消一部分数,最后可以得到公式的主体部分为n*(n+m-2)*(n+m-2)*...(n-m+2)/m!;
然后就是乘法逆元,将m!逆元,乘法逆元,找度娘。
这个题写的好讨厌,老是小细节出问题,wa了好几好几发_(:з」∠)_
一开始没有将公式优化,也没有用逆元,直接就是超时_(:з」∠)_,改了无数次终于改对了,太菜了,QAQ。
代码解释:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N=1e5+10; 5 const int mod=998244353; 6 ll qpow(ll x, int q){ //乘法逆元 7 ll res = 1; 8 while(q){ 9 if(q%2) res = res*x%mod; 10 x = x*x%mod; 11 q /= 2; 12 } 13 return res; 14 } 15 int main(){ 16 int n,m; 17 ll ans; 18 while(~scanf("%d%d",&n,&m)){ 19 if(m>n)printf("0 "); //x的次方数最大为n次,超过了就不存在 20 else if(n%2==1&&m%2==0||n%2==0&&m%2==1)printf("0 "); //n和m奇偶性不同的时候结果为0 21 else if(n==0&&m==0)printf("1 "); //如果n和m为0,结果为1 22 else if(m==0){ //如果m为0,就是有规律的 23 if(n%2==1)printf("0 ");//如果为奇数,就是0 24 else if(n%2==0){ //如果为偶数 25 if((n/2)%2==1)printf("998244352 ");//除以2之后如果为奇数就是-1,(-1+mod)%mod结果就是这个数 26 else printf("1 ");//除以2之后如果为偶数就是1 27 } 28 } 29 else{ //其他的通过公式进行计算 30 ans=1; 31 for(int i=n-m+2;i<=n+m-2;i+=2) //优化之后只需要进行部分操作就可以 32 ans=(ans*i)%mod;//二阶乘 33 ans=(ans*n)%mod;//公式 34 ll temp=1; 35 for(int i=1;i<=m;i++) 36 temp=(i*temp)%mod;//m的阶乘 37 ll cnt; 38 cnt=qpow(temp,mod-2);//m的阶乘的逆元 39 //cout<<"aaaaaaaaaaaaaaaa"<<endl; 40 ans=ans*cnt%mod;//将结果进行相乘 41 ans=((n-m)/2)%2==0?ans:-ans;//判断正负号 42 ans=(ans+mod)%mod; 43 printf("%lld ",ans%mod); 44 } 45 } 46 return 0; 47 }
作为一个数学渣,做这种题目简直要命_(:з」∠)_
这个题也没用到什么很厉害的算法,就是数学题,大佬们肯定很easy的就过了_(:з」∠)_
加油_(:з」∠)_