Description
沫沫最近在玩一个二维的射箭游戏,如下图 1 所示,这个游戏中的 x 轴在地面,第一象限中有一些竖直线段作为靶子,任意两个靶子都没有公共部分,也不会接触坐标轴。沫沫控制一个位于(0,0)的弓箭手,可以朝 0 至 90?中的任意角度(不包括 0度和 90度),以任意大小的力量射出带有穿透能力的光之箭。由于游戏中没有空气阻力,并且光之箭没有箭身,箭的轨迹会是一条标准的抛物线,被轨迹穿过的所有靶子都认为被沫沫射中了,包括那些 只有端点被射中的靶子。这个游戏有多种模式,其中沫沫最喜欢的是闯关模式。在闯关模式中,第一关只有一个靶 子,射中这个靶子即可进入第二关,这时在第一关的基础上会出现另外一个靶子,若能够一箭 双雕射中这两个靶子便可进入第三关,这时会出现第三个靶子。依此类推,每过一关都会新出 现一个靶子,在第 K 关必须一箭射中前 K 关出现的所有 K 个靶子才能进入第 K+1 关,否则游戏 结束。沫沫花了很多时间在这个游戏上,却最多只能玩到第七关“七星连珠”,这让她非常困惑。 于是她设法获得了每一关出现的靶子的位置,想让你告诉她,最多能通过多少关
Solution
我们需要确定的是 (a,b) 的取值,考虑求取值范围
对于每一条直线 ((x,y1,y2)):
(y1<=a*x^2+b*x<=y2)
移向得:
(b>=frac{y1}{x}-x*a)
(b<=frac{y2}{x}-x*a)
这相当于求点 ((a,b)) 取值范围,加上这两个限制之后就是一个半平面
我们要判断的就是是否对于每一个直线的半平面存在一个交
写一个半平面交就好了,大致思想是维护一个这样的东西:
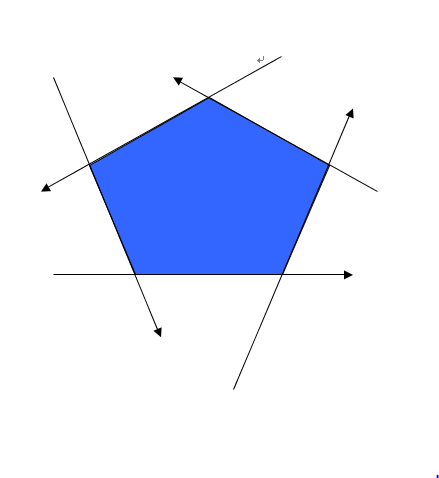
我们假设沿着每一条直线的正方向看去,左半平面的都是合法的半平面
我们新加入一条直线时,就判断队尾和队首的交点是否在直线的左半平面即可,不满足则弹掉
注意弹的顺序一定是先弹 (r) 再弹 (l),因为新加入的直线和 (r) 这条直线的交点才是凸包上的点
另外就是叉积求直线交点:
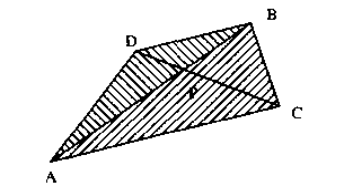
大致思想是用:
(frac{S△DAB}{S△ABC}=frac{DP}{PC})
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;const double inf=1e12;
struct P{double x,y;P(){}P(double _x,double _y){x=_x;y=_y;}};
inline double Y(double x,double y,double a){return y/x-x*a;}
struct line{P a,b;int id;double p;}l[N],e[N],q[N];
inline double operator *(P a,P b){return a.x*b.y-a.y*b.x;}
inline P operator -(P a,P b){return P(a.x-b.x,a.y-b.y);}
inline P cross(line a,line b){
double s1=(a.b-a.a)*(b.a-a.a);
double s2=(b.b-a.a)*(a.b-a.a);
double t=s1/(s1+s2);
return P(b.a.x+t*(b.b.x-b.a.x),b.a.y+t*(b.b.y-b.a.y));
}
inline bool comp(line i,line j){
return i.p!=j.p?i.p<j.p:(i.b-i.a)*(j.b-i.a)>0;
}
int n,m=0;
inline bool judge(line a,line b,line c){
P d=cross(a,b);
return (d-c.a)*(c.b-c.a)>-1e-7;
}
inline bool check(int mid){
int cnt=0,L=1,R=0;
for(int i=1;i<=m;i++)
if(l[i].id<=mid){
if(l[i].p!=e[cnt].p)cnt++;
e[cnt]=l[i];
}
q[++R]=e[1];q[++R]=e[2];
for(int i=3;i<=cnt;i++){
while(L<R && judge(q[R],q[R-1],e[i]))R--;
while(L<R && judge(q[L],q[L+1],e[i]))L++;
q[++R]=e[i];
}
while(L<R&&judge(q[R-1],q[R],q[L]))R--;
while(L<R&&judge(q[L+1],q[L],q[R]))L++;
return R-L>1;
}
int main(){
freopen("pp.in","r",stdin);
freopen("pp.out","w",stdout);
cin>>n;
int x,y1,y2;
l[++m].a=P(-inf,-inf);l[m].b=P(inf,-inf);
l[++m].a=P(inf,-inf);l[m].b=P(inf,inf);
l[++m].a=P(inf,inf);l[m].b=P(-inf,inf);
l[++m].a=P(-inf,inf);l[m].b=P(-inf,-inf);
for(int i=1;i<=n;i++){
scanf("%d%d%d",&x,&y1,&y2);
l[++m].a=P(-1,Y(x,y1,-1));l[m].b=P(1,Y(x,y1,1));l[m].id=i;
l[++m].a=P(1,Y(x,y2,1));l[m].b=P(-1,Y(x,y2,-1));l[m].id=i;
}
for(int i=1;i<=m;i++)l[i].p=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x);
sort(l+1,l+m+1,comp);
int l=1,r=n,mid,ans=0;
while(l<=r){
mid=(l+r)>>1;
if(check(mid))ans=mid,l=mid+1;
else r=mid-1;
}
cout<<ans<<endl;
return 0;
}