• 分配问题与Hungarian算法

    分配问题与Hungarian算法

    分配问题
    指派问题
    匈牙利算法

    匈牙利方法是一种能够在多项式时间内解决分配问题(assignment problem)的组合优化算法。它由Harold Kuhn 与1955年发展并提出，由于该算法很大程度上依赖于先前两位匈牙利数学家:Denes Konig 和 Jeno Egervary,所以被命名为“匈牙利方法”。
    1957年James Munkres重新审视了这个方法，证明发现该方法是严格polynomial的，所以之后该方法也被称为Kuhn-Munkres 算法或者Munkres分配算法。原始的匈牙利算法的时间复杂度是,然而之后Edmonds和Karp，以及Tomizawa独立发现经过一定的修改，该算法能改达到的时间复杂度。 Ford和Fulkerson将该方法扩展到一般运输问题的求解上。 2006年，研究发现Carl Custav Jacobi在19实际就解决了assignment问题，并且在其逝世后的1890年求解过程被以拉丁语形式发表。。。

    指派问题

    匈牙利法解决的指派问题应该具有两个约束条件

    • workes 和tasks的数目应该相同，即o2o问题。

    • 求解的是最小化问题，如工作时间的最小化、费用的最小化等等

    指派问题示例：
    有三个workers: Jim, Steve和Alan，现在有3个工作：clean the bathroom, sweep the floors和wash the windows需要交给这三个人，每个人只能完成一个任务，对应的cost matrix如下

    --- Clean bathroom Sweep floors Wash windows
    Jim $2 $3 $3
    Steve $3 $2 $3
    Alan $3 $3 $2

    那么如何分配任务是开销最小就是一个指派问题

    匈牙利法步骤

    问题： 假定某单位有甲、乙、丙、丁、戊五个员工，现需要完成A、B、C、D、E五项任务，每个员工完成某项任务的时间如下图所示，应该如何分配任务，才能保证完成任务所需要的时间开销最小？

    enter description here

    1476015762594.jpg

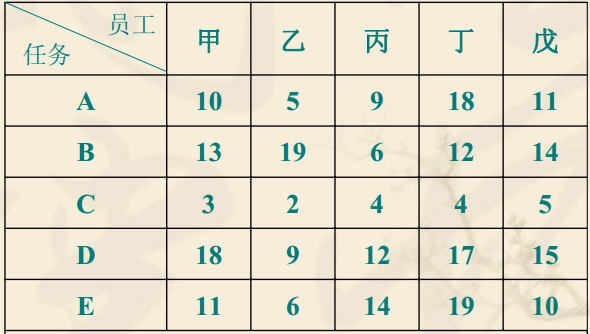
    解：

    1. 写出系数矩阵

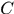
    2. 更新系数矩阵，使系数矩阵的每一行每一列都减去该行该列的最小值，保证每一行每一列都有0元素出现,参见定理2.

    3. 选择只有一个0元素的行或列将该0元素标注为独立0元素，并将该0元素所在的列或行中0元素划掉，直至找不到满足条件的行或列，需要注意的是在循环时，划掉的0元素不再视为0元素。比如我们找下面这个系数矩阵的标注0元素和划掉的0元素

    那么我们用1表示0元素，0表示非0元素，用2标注独立0元素，-2表示划掉0元素，依次得到的中间结果为

    可以发现我们在标注第一行第2个0元素时，并没有把已经划掉的第一个0当作0元素看待。

    1. 划盖0线。
      a. 首先找到不含有独立0元素的行，将行标注 (4)
      b. 找到标注行中划掉的0元素所在的列，将列标注 (2,3)
      c. 将标注列中独立0元素所在的行标注 (4, 1, 2)
      d. 重复b,c步骤知道所有的标注行中不再存在划掉的0元素
      (行：4 ,1, 2, 3 ; 列: 2, 3, 1)
      e. 在所有标注的列上做盖0线，在所有未被标注的行上做盖0线，我们在矩阵中用3表示被盖0线覆盖，则

      可以发现所有的0元素都被覆盖掉，所以称为盖0线。
      根据定理1，如果此时盖0线的个数等于矩阵的维数，相当于找到n个独立0元素，则跳到步骤7，否则步骤5更新系数矩阵。

    2. 更新系数矩阵。
      a. 找到未被盖0线覆盖的元素中的最小值
      b. 所有未被盖0线覆盖的元素减去最小值
      c. 所有盖0线交叉处的元素值加上最小值

    3. 重复步骤4，5

    4. 计算最优解。
      类似步骤3中找独立0元素的方法在C中找到n个不同行不同列的0元素所对应的位置。

    定理1. 系数矩阵C中独立零元素的最多个数等于能覆盖所有零元素的最少线数。 —— D. Konig
    定理2. 若将分配问题的系数矩阵每一行及每一列分别减去各行及各列的最小元素，则新的分配问题与原分配问题有相同的最优解，只是最优值差一个常数。

    当然，注意找盖〇线的方法并不是唯一的，比如下述方法

    1. 同上一方法

    2. 同上一方法

    3. 在C中寻找未被盖〇线覆盖的存在0元素且数组最少的行(列)，标注一个0元素作为独立0元素，该0元素所在的列(行)做盖0线。重复此步骤，直至找不到符合条件的行或列，已经被找过的行(列)就不再找了！

    4. 若是盖0线数组等于矩阵维度，则跳到7

    5. 同上一方法

    6. 重复3，4，5

    7. 同上一方法

    当然还有别的方法，比如从包含最多0元素的行或列开始做盖0线直到将所有的0元素覆盖掉等

    这里代码实现了上面两个方法，注释掉的是第二个方法的核心

    1. function [cost,CMatrix]=Assignment(C,ismin) 
    2. % Assignment problem solved by hungarian method. 
    3. % 
    4. % input: 
    5. % C - 系数矩阵，可以适应workers和tasks数目不同的情形 
    6. % ismin - 1表示最小化问题，0表示最大化问题 
    7. % ouput: 
    8. % cost - 最终花费代价 
    9. % CMatrix - 对应的匹配矩阵，元素1所在位置c_{ij}表示j task分配给 i worker。 
    10. % 
    11.  
    12. [m,n]=size(C); 
    13. if ismin==0 
    14. C=max(C(:))-C; 
    15. end 
    16.  
    17. %workes 和tasks数目不相同 
    18. if m<n 
    19. C=[C;zeros(n-m,n)]; 
    20. elseif m>n 
    21. C=[C zeros(m,m-n)]; 
    22. end 
    23. copyC=C; 
    24. d=max(m,n);% 最终系数矩阵的维度 
    25. C=C-repmat(min(C,[],2),1,d); 
    26. C=C-repmat(min(C,[],1),d,1); 
    27.  
    28. %% 方法一 
    29. while 1 
    30. A=int8((C==0)); 
    31. nIZeros=0; % 独立0元素的个数 
    32. while 1 
    33. r=sum(A==1,2); % 每一行0元素的个数 
    34. [~,idr]=find(r'==1);%找到只有一个0元素的行 
    35. if ~isempty(idr) % 如果找到这样的行 
    36. tr=A(idr(1),:); 
    37. [~,idc]=find(tr==1);%找到0元素所在列 
    38. A(idr(1),idc)=2;%标注独立元素 
    39. tc=A(:,idc); 
    40. tc(idr(1))=2; 
    41. [~,idr]=find(tc'==1);%找到独立0元素所在列的其他0元素 
    42. A(idr,idc)=-2;%划掉独立0元素所在列的其余0元素 
    43. nIZeros=nIZeros+1; 
    44. else 
    45. c=sum(A==1,1); % 每一列0元素的个数 
    46. [~,idc]=find(c==1);%找到只含有一个0元素的列 
    47. if ~isempty(idc)% 找到这样的列 
    48. tc=A(:,idc(1)); 
    49. [~,idr]=find(tc'==1);%0元素所在的行 
    50. A(idr,idc(1))=2;%标注独立0元素 
    51. tr=A(idr,:); 
    52. tr(idc(1))=2; 
    53. [~,idc]=find(tr==1);%独立0元素所在行的其他0元素 
    54. A(idr,idc)=-2;%划掉独立0元素所在行的其余0元素 
    55. nIZeros=nIZeros+1; 
    56. else 
    57. break; 
    58. end 
    59. end 
    60. end 
    61.  
    62. if nIZeros==d 
    63. %计算最优解 
    64. CMatrix=(A==2); 
    65.  
    66. if ismin==1 
    67. cost=sum(copyC(:).*CMatrix(:)); 
    68. else 
    69. cost = sum((max(copyC(:))-copyC(:)).*CMatrix(:)); 
    70. end 
    71. CMatrix=CMatrix(1:m,1:n); 
    72. break;%找到d个独立0元素，则跳出循环 
    73. else% 独立0元素个数不足，就要找盖0线了 
    74. r=sum(A==2,2); 
    75. [~,idr]=find(r'==0);%不含有独立0元素的行 
    76. idrr=idr; 
    77. idcc=[]; 
    78. while 1 
    79. tr=A(idrr,:); 
    80. [~,idc]=find(tr==-2);%不含独立0元素的行中划掉的0元素所在列 
    81. if isempty(idc),break;end 
    82. tc=A(:,unique(idc)); 
    83. [idrr,~]=find(tc==2);%这些列中标注的0元素所在行 
    84. idr=[idr,idrr']; 
    85. idcc=[idcc,idc]; 
    86. end 
    87. idry=1:d; 
    88. idry(idr)=[];%盖0线所在的行索引 
    89. TempC=C;%存储非覆盖元素 
    90. TempC(idry,:)=[]; 
    91. TempC(:,idcc)=[]; 
    92. minUnOverlap=min(TempC(:)); 
    93. %更新系数矩阵 
    94. C=C-minUnOverlap; 
    95. C(idry,:)=C(idry,:)+minUnOverlap; 
    96. C(:,idcc)=C(:,idcc)+minUnOverlap; 
    97. end 
    98. end 
    99. %% 方法二 
    100. % while 1 
    101. % CMatrix=zeros(d); 
    102. % nLines=0; 
    103. % A=(C==0); 
    104. % idx=[]; 
    105. % idy=[]; 
    106. % sr=[]; 
    107. % sc=[]; 
    108. % while 1 
    109. % r=sum(A,2); 
    110. % c=sum(A,1); 
    111. % r(sr)=0; 
    112. % c(sc)=0; 
    113. % trc=[r(:);c(:)]; 
    114. % [trc,idtrc]=sort(trc,1,'ascend'); 
    115. % [~,idn0]=find(trc'>0); 
    116. % if ~isempty(idn0) 
    117. % id=idtrc(idn0(1)); 
    118. % if id>d 
    119. % tc=A(:,id-d); 
    120. % [~,idr]=find(tc'==1); 
    121. % A(idr(1),:)=0;  
    122. % nLines=nLines+1; 
    123. % idy=[idy,idr(1)]; 
    124. % CMatrix(idr(1),id-d)=1; 
    125. % sc=[sc,id-d]; 
    126. % else 
    127. % tr=A(id,:); 
    128. % [~,idc]=find(tr==1); 
    129. % A(:,idc(1))=0; 
    130. % nLines=nLines+1; 
    131. % idx=[idx,idc(1)]; 
    132. % CMatrix(id,idc(1))=1; 
    133. % sr=[sr,id]; 
    134. % end  
    135. % else 
    136. % break; 
    137. % end 
    138. % end 
    139. % if nLines==d 
    140. % if ismin 
    141. % cost=sum(copyC(:).*CMatrix(:)); 
    142. % else 
    143. % cost=sum((max(copyC(:))-copyC(:)).*CMatrix(:)); 
    144. % end 
    145. % CMatrix=CMatrix(1:m,1:n); 
    146. % break; 
    147. % else 
    148. % tempC=C; 
    149. % tempC(idy,:)=[]; 
    150. % tempC(:,idx)=[]; 
    151. % minUnOverlap=min(tempC(:)); 
    152. % C=C-minUnOverlap; 
    153. % C(idy,:)=C(idy,:)+minUnOverlap; 
    154. % C(:,idx)=C(:,idx)+minUnOverlap; 
    155. % end 
    156. % end 
    157.  
    158. end 
    159.  

    匈牙利算法的拓展

    • workers数小于tasks数目
      此时可以虚拟出若干个workers使个数相等，对于虚拟出的workers对于tasks的代价是相同的都是0.

    • workers数目大于tasks数目
      可以和上述类似，增加虚拟tasks，在系数矩阵中对应列元素都为0

    • 最大值问题
      找到系数矩阵中最大的元素，然后使用最大元素分别减去矩阵中元素，这样最大化问题就化为最小化问题，同样可以使用匈牙利算法。

    测试

    1. 现在使用代码求解上述例题

    enter description here

    1476016827034.jpg

    1. 注意方法一中存在不足之处是必须找到仅含一个0元素的行或列，这并不科学，比如下面这个系数矩阵，就会出现死循环，所以可以寻找含有最少0元素的行或列，这就和方法二类似了，所以我没再实现。方法二可以解决下面这个极端例子

    我们来使用方法二(将代码中注释掉的部分反注释，方法一注释掉)测试下这个极端的例子

    enter description here

    1476017296572.jpg

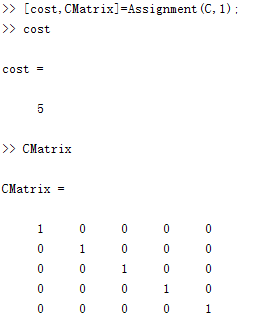
    1. 测试下面这个系数矩阵，匈牙利算法拓展1

    enter description here

    1476017394268.jpg

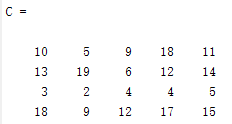
    结果

    enter description here

    1476017434080.jpg

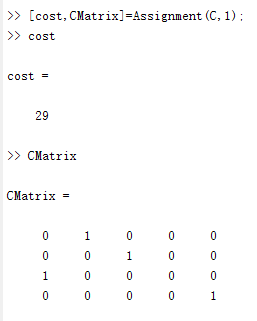
    1. 对上个测试用例计算最大代价

    enter description here

    1476017934004.jpg

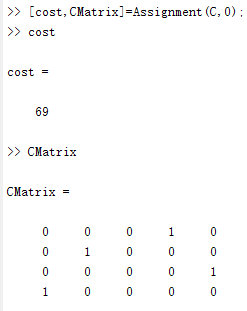
    综上，相较于方法一，方法二能够处理各种状况。
  • 相关阅读:
    构建简单的二叉树（C）
    C指針淺析（3）
    C語言函數
    C# 細節（2）
    如何做好软件架构设计
    C# 細節（1）
    .NET Framework格式化字符串
    Windows下通过删除硬盘分区直接强行移除Fedora后恢复Windows启动项的方法
    DreamWeaver使用技巧学习心得
    MyEclipse使用心得、快捷键、设置
  • 原文地址：https://www.cnblogs.com/YiXiaoZhou/p/5943775.html
Copyright © 2020-2023  润新知