能推出一些性质。
矩形肯定是全部躺着或全部立着比较优。
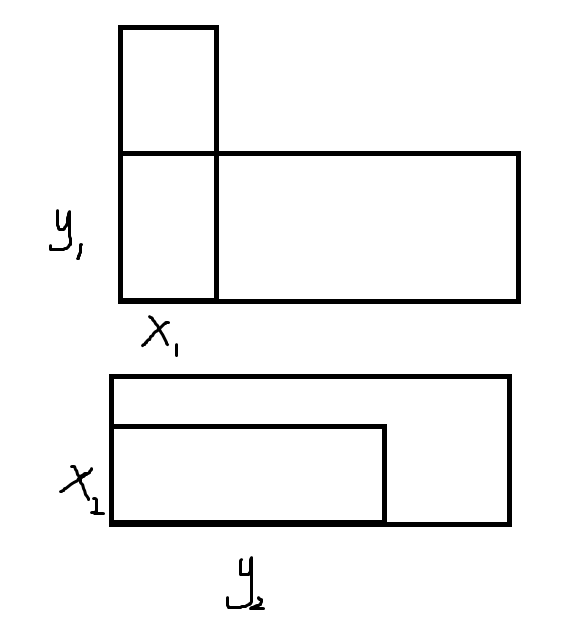
如图x1显然等于x2,y1显然小于y2。
所以我们就让它们都躺下吧。
然后一定有一组的宽为宽最小的矩形的宽。
然后我们枚举另一组的宽最小的矩形。(当然宽在最小的矩形和枚举的矩形之间的矩形都跟宽最小的矩形一组)
之后就只剩下长的影响了。
假设现在还剩下这些长度(排好序):
1 2 3 4 5 6 7 8 9
当然是把一段的矩形分在一组比较优。
那么分在哪一组呢?都试一下不就行了。
用平衡树维护k小。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<ctime>
#include<cstdlib>
using namespace std;
const int N=201000;
struct node{
int x,y;
}c[N];
bool cmp(node a,node b){
return a.x<b.x;
}
int tot,rad[N],size[N],val[N],ch[N][2],root,x,y,z;
int new_node(int x){
int now=++tot;
rad[now]=rand();
size[now]=1;
val[now]=x;
return now;
}
void update(int now){
size[now]=size[ch[now][0]]+size[ch[now][1]]+1;
}
int merge(int x,int y){
if(!x||!y)return x+y;
if(rad[x]>rad[y]){
ch[x][1]=merge(ch[x][1],y);
update(x);
return x;
}
else{
ch[y][0]=merge(x,ch[y][0]);
update(y);
return y;
}
}
void split(int &x,int &y,int now,int k){
if(now==0)x=y=0;
else{
if(val[now]<=k){
x=now;
split(ch[x][1],y,ch[x][1],k);
}
else{
y=now;
split(x,ch[y][0],ch[y][0],k);
}
update(now);
}
}
int kth(int now,int k){
int l=ch[now][0];
if(size[l]>=k)return kth(l,k);
else if(size[l]+1==k)return val[now];
else return kth(ch[now][1],k-size[l]-1);
}
int read(){
int sum=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){sum=sum*10+ch-'0';ch=getchar();}
return sum*f;
}
int n;
long long ans;
int main(){
srand(time(NULL));
n=read();
for(int i=1;i<=n*2;i++){
c[i].x=read(),c[i].y=read();
if(c[i].x>c[i].y)swap(c[i].x,c[i].y);
}
sort(c+1,c+1+n*2,cmp);
for(int i=3;i<=n*2;i++){
split(x,y,root,c[i].y);
root=merge(x,merge(new_node(c[i].y),y));
}
for(int i=2;i<=n;i++){
int mn=kth(root,1);
int Mn=kth(root,n-(i-1)+1);
ans=max(ans,1ll*c[1].x*1ll*min(1ll*mn,1ll*c[1].y)+1ll*c[i].x*1ll*min(1ll*Mn,1ll*c[i].y));
Mn=kth(root,n);
ans=max(ans,1ll*c[i].x*1ll*min(1ll*c[i].y,1ll*mn)+1ll*c[1].x*1ll*min(1ll*c[1].y,1ll*Mn));
split(x,z,root,c[i+1].y);
split(x,y,x,c[i+1].y-1);
y=merge(ch[y][0],ch[y][1]);
root=merge(merge(x,y),z);
c[1].y=min(c[1].y,c[i].y);
}
printf("%lld",max(ans,1ll*c[1].x*c[1].y+1ll*c[n+1].x*min(1ll*c[n+1].y,1ll*kth(root,1))));
return 0;
}