【题解】C2Crni - Crni [COCI2010] [SP7884]
传送门:( ext{C2Crni - Crni}) ( ext{[COCI2010]}) ( ext{[SP7884]})
【题目描述】
给定一个 ( ext{N} * ext{N}) 的矩阵,每个格子要么为白色((B))要么为黑色((C))。定义黑矩形为所含单元格数大于等于 (2) 且所含单元格均为黑色的矩阵。
如图:

左边的两个矩形都不是黑矩形,因为 (1) 中有白格,(2) 的大小为 (1),而右图的 (3) 个都是黑矩形。
要解决的问题是在给定的矩形中找出两个没有共公部分的黑矩形,输出所有方案数,由于数较大,答案对 (10007) 取模。
【样例】
样例输入:
2
CC
CC
样例输出:
2
样例输入:
3
CCB
CCB
CBB
样例输出:
5
样例输入:
5
BCCBB
BBCBB
BCCBB
BBBBB
CCBBB
样例输出:
8
【数据范围】
(100 \%:) (1 leqslant n leqslant 1000)
【分析】
这是一道套路题,用到了很多关于矩阵的处理技巧,但找到解决方法后会发现它的思维难度其实并不高,主要是代码实现较困难,所以也可以视其为膜你题。
【前缀和的套路】
找子矩阵基本都会用到前缀和,常见的查询子矩阵可以直接容斥,例如维护二维树状数组时用到的方法:
设 (S[x][y]=sum_{i=1}^{x} sum_{j=1}^{y} a[i][j]),那么递推式为 (S[i][j]=) (S[i-1][j]+S[i][j-1]-S[i-1][j-1]+a[i][j])
如果要查询以 ((x1,y1)) 为左下角,以 ((x2,y2)) 为右下角的矩阵和,(sum_{i={x_1}}^{y_1} sum_{j={x_2}}^{y_2} a[i][j]=) (S[x2][y2]-S[x1-1][y2]-S[x2][y1-1]+S[x1-1][y1-1])
在预处理式子时需要从左上角一直递推到右下角,而稍复杂一点的需要统计多个方向(没错,就是此题了),即从最多 (4) 个角落(左上,左下,右上,右下)开始向其对角处递推,得到多个助于统计答案的前缀和数组。
【预处理】
回到此题。
为方便处理,将矩阵中的黑点设为 (1),白点设为 (0) 。
对于所有的黑点,先预处理出 (4) 个数组:
((1).) (RD[i][j]): 以 ((i,j)) 为右下角的黑矩阵个数。
((2).) (LU[i][j]): 以 ((i,j)) 为左上角的黑矩阵个数。
((3).) (LD[i][j]): 以 ((i,j)) 为左下角的黑矩阵个数。
((4).) (RU[i][j]): 以 ((i,j)) 为右上角的黑矩阵个数。
但如果暴力枚举的话 (O(n^4)) 复杂度过高,需要考虑合理继承前面求出的信息。
以 (RD) 为例,为便于推导,我们先在矩阵中枚举一条辅助线,假设已经求出了第 (i) 行前 (j-1) 列的 (RD) 信息,如图为 (i=4,j=4) 的情况:
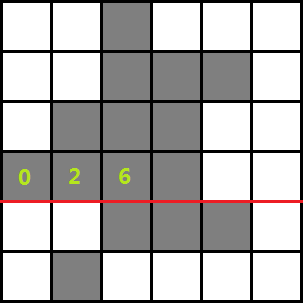
定义 (H[i][j]) 为点 ((i,j)) 向上最多可以延伸的距离(或者说高度),如果 (a(i,j)) 为白块,(H[i][j]=0) 。
处理方法如下:
对于点 ((i,j)) 找到同一列前面第一个 (H) 小于它的位置 ((i,k))。
由于 ([k+1,j]) 的高度都大于 (j),那么将会有 (H[i][j]*(j-k)) 个点可以作为黑矩形的左上角(右下角为 ((i,j))),但是将 ((i,j)) 自己作为左上角时黑矩阵大小只有 (1),所以要减去 (1) 。
另外以 ((i,k)) 为右下角的黑矩阵都可以将长度扩大 (j-k),即变成以 ((i,j)) 为右下角,但以 ((i,k)) 为右下角的情况没有计算在 (RD[i][k]) 以内,所以要加上 (1) 。
得到递推式为:(RD[i][j]=H[i][j]*(j-k)-1+RD[i][k]+1) 。
于是时间复杂度就被优化到了 (O(n^3)),但还不够优秀。
现在的问题是如何快速找 (k),方法同 ( ext{Largest}) ( ext{Rectangle}) ( ext{in}) ( ext{a}) ( ext{Histogram}) (题解),直接单调栈维护即可。
在上面那张图中 (H[4][1]=1,H[4][2]=2,H[4][3]=4,H[4][4]=3),所以 (j=4) 时的决策点 (k=2),因此 (RD[3][4]=3*2-1+RD[3][2]+1) 。
同理可得 (LU,LD,RU) 。
【统计答案】
依旧是枚举辅助线:
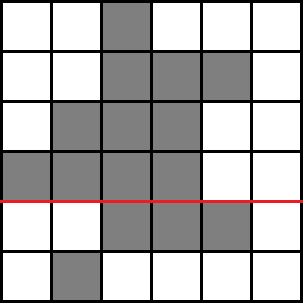
先求出下边界在红线上面的黑矩形个数,即 (sum_{i=1}^{x} sum_{j=1}^{n} RD[i][j])(或者 (LD[i][j])),
再求出上边界紧贴在红线下面的黑矩阵个数,即 (sum_{j=1}^{n}LU[x+1][j])(或者 (RU[x+1][j])),
将二者相乘,再对于每一条辅助线算出的结果求和,得到相对位置为上下的黑矩形总对数。(其实也可以固定红线上面,红线下面求总个数)
同理枚举竖线,可得相对位置为左右的黑矩形总对数。
但这样会有算重复的情况,如下图绿色部分和蓝色部分:

因此还要减去相对位置既有上下又有左右的黑矩形对数,也就是在十字线对角象限的黑矩形对数,求法和前面大致相同。为方便处理,要任选两个方向计算矩阵前缀和(递推式和二维树状数组的一样):
((1).) (S_{RD}[x][y]=sum_{i=1}^{x} sum_{j=1}^{y} RD[i][j])
前缀和递推方向:左上 ( ext{→}) 右下 。
矩阵前缀和意义:右下角在 ((i,j)) 左上面的黑矩阵个数。
((2).) (S_{LU}[x][y]=sum_{i=n}^{x} sum_{j=n}^{y} RD[i][j])
前缀和递推方向:右下 ( ext{→}) 左上 。
矩阵前缀和意义:左上角在 ((i,j)) 右下面的黑矩阵个数。
((3).) (S_{LD}[x][y]=sum_{i=1}^{x} sum_{j=n}^{y} RD[i][j])
前缀和递推方向:右上 ( ext{→}) 左下 。
矩阵前缀和意义:左下角在 ((i,j)) 右上面的黑矩阵个数。
((4).) (S_{RU}[x][y]=sum_{i=n}^{x} sum_{j=1}^{y} RD[i][j])
前缀和递推方向:左下 ( ext{→}) 右上 。
矩阵前缀和意义:右上角在 ((i,j)) 左下面的黑矩阵个数。
最后,此题细节较多,变量名没设好的话很容易搞混。
时间复杂度为:(O(n^2)) 。
【Code】
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#define Re register int
#define For(i,a,b) for(Re i=a;i<=b;++i)
#define Por(i,a,b) for(Re i=a;i>=b;--i)
#define print() for(Re i=1;i<=n;puts(""),++i)for(Re j=1;j<=n;++j)
using namespace std;
const int N=1003,P=10007;
int n,Q[N],A[N][N],H[N][N],SS[N][N];char ch[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
int RD[N][N];
inline void get_RD(){//RD[i][j]: 以i,j为右下角的黑矩形个数(1,1)→(n,n)
memset(H,0,sizeof(H));
For(i,1,n)For(j,1,n)if(A[i][j])H[i][j]=H[i-1][j]+1;
// print()printf("%d ",H[i][j]);puts("");
For(i,1,n){
Re h=1,t=0;
For(j,1,n)if(!A[i][j])RD[i][j]=-1;
RD[i][Q[++t]=0]=-1;
For(j,1,n){
while(h<=t&&H[i][Q[t]]>=H[i][j])--t;
if(h<=t&&A[i][j])RD[i][j]=RD[i][Q[t]]+1+H[i][j]*(j-Q[t])-1;
Q[++t]=j;
}
For(j,1,n)if(RD[i][j]<0)RD[i][j]=0;
}
// print()printf("%d ",RD[i][j]);puts("");
}
int LU[N][N];
inline void get_LU(){//LU[i][j]: 以i,j为左上角的黑矩形个数(n,n)→(1,1)
memset(H,0,sizeof(H));
Por(i,n,1)Por(j,n,1)if(A[i][j])H[i][j]=H[i+1][j]+1;
// print()printf("%d ",H[i][j]);puts("");
Por(i,n,1){
Re h=1,t=0;
Por(j,n,1)if(!A[i][j])LU[i][j]=-1;
LU[i][Q[++t]=n+1]=-1;
Por(j,n,1){
while(h<=t&&H[i][Q[t]]>=H[i][j])--t;
if(h<=t&&A[i][j])LU[i][j]=LU[i][Q[t]]+1+H[i][j]*(Q[t]-j)-1;
Q[++t]=j;
}
Por(j,n,1)if(LU[i][j]<0)LU[i][j]=0;
}
// print()printf("%d ",LU[i][j]);puts("");
}
int LD[N][N];
inline void get_LD(){//LD[i][j]: 以i,j为左下角的黑矩形个数(1,n)→(n,1)
memset(H,0,sizeof(H));
For(i,1,n)Por(j,n,1)if(A[i][j])H[i][j]=H[i-1][j]+1;
// print()printf("%d ",H[i][j]);puts("");
For(i,1,n){
Re h=1,t=0;
Por(j,n,1)if(!A[i][j])LD[i][j]=-1;
LD[i][Q[++t]=n+1]=-1;
Por(j,n,1){
while(h<=t&&H[i][Q[t]]>=H[i][j])--t;
if(h<=t&&A[i][j])LD[i][j]=LD[i][Q[t]]+1+H[i][j]*(Q[t]-j)-1;
Q[++t]=j;
}
Por(j,n,1)if(LD[i][j]<0)LD[i][j]=0;
}
// print()printf("%d ",LD[i][j]);puts("");
}
int RU[N][N];
inline void get_RU(){//RU[i][j]: 以i,j为右上角的黑矩形个数(n,1)→(1,n)
memset(H,0,sizeof(H));
Por(i,n,1)Por(j,n,1)if(A[i][j])H[i][j]=H[i+1][j]+1;
// print()printf("%d ",H[i][j]);puts("");
Por(i,n,1){
Re h=1,t=0;
For(j,1,n)if(!A[i][j])RU[i][j]=-1;
RU[i][Q[++t]=0]=-1;
For(j,1,n){
while(h<=t&&H[i][Q[t]]>=H[i][j])--t;
if(h<=t&&A[i][j])RU[i][j]=RU[i][Q[t]]+1+H[i][j]*(j-Q[t])-1;
Q[++t]=j;
}
For(j,1,n)if(RU[i][j]<0)RU[i][j]=0;
}
// print()printf("%d ",RU[i][j]);puts("");
}
inline int U_D(){//加上-下
Re ans=0,S=0;
For(i,1,n){
For(j,1,n)(ans+=S*LU[i][j]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定在辅助线下面
For(j,1,n)(S+=RD[i][j])%=P;//用【右下角为(i,j)的矩阵RD】求辅助线上边的总个数
}
return ans%P;
}
inline int L_R(){//加左-右
Re ans=0,S=0;
For(j,1,n){
For(i,1,n)(ans+=S*LU[i][j]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定在辅助线右边
For(i,1,n)(S+=RD[i][j])%=P;//用【右下角为(i,j)的矩阵RD】求辅助线左边的总个数
}
return ans%P;
}
inline int LU_RD(){//减左上-右下
Re ans=0;memset(SS,0,sizeof(SS));
For(i,1,n-1)For(j,1,n-1){
SS[i][j]=((RD[i][j]+SS[i-1][j]+SS[i][j-1])%P-SS[i-1][j-1]+P)%P;
//十字线左上角的用【右下角为(i,j)的矩阵RD】求总和
(ans+=SS[i][j]*LU[i+1][j+1]%P)%=P;//用【左上角为(i,j)的矩阵LU】固定十字线的右下角
}
return ans;
}
inline int RU_LD(){//减右上-左下
Re ans=0;memset(SS,0,sizeof(SS));
For(i,1,n-1)Por(j,n,2){
SS[i][j]=((LD[i][j]+SS[i-1][j]+SS[i][j+1])%P-SS[i-1][j+1]+P)%P;
//十字线右上角的用【左下角为(i,j)的矩阵LD】求总和
(ans+=SS[i][j]*RU[i+1][j-1]%P)%=P;//用【右上角为(i,j)的矩阵RU】固定十字线的左下角
}
return ans;
}
int main(){
// freopen("crni.in","r",stdin);
// freopen("crni.out","w",stdout);
in(n);
For(i,1,n){
scanf("%s",ch+1);
For(j,1,n)A[i][j]=(ch[j]=='C');
}
get_RD(),get_LU(),get_LD(),get_RU();
printf("%d
",((U_D()+L_R())%P-(LU_RD()+RU_LD())%P+P)%P);
// fclose(stdin);
// fclose(stdout);
return 0;
}