浅谈简单线性dp

简单动态规划

前言

简单的动态规划其实并不是很难，在初期确实感觉无从下手，就是感觉为什么明明很简单却总是做不出来，其实就是对动态规划的本质理解较差，从而很难推断出状态方程进行转移，或者找到突破点，其实如果是没有算法的简单动态规划，题做多了就容易找到感觉了。

做题通法

首先找最初始状态，然后寻找一下其他状态，然后我们在找到最优状态时可以遇到更优秀的解或者就没有解，如果更优秀，就记录下来，如果没有之前记录的优秀，那么就没有必要再继续了，除非对答案贡献相同并且状态却不一样（比如图上方向不一样），那么就可以考虑继续沿着此状态.

dp,记忆化搜索，递推，前缀和，其实本质是一样的。

提高的唯一方法——通过独立做题，进行独立思考

最大多段不重合子序列和

当我连最大子序列和都做不出来时，我却以为我已经熟练掌握dp了。

看到本题觉得很难，但是先看最简单的，假设只是一段，只让你求一段的最大子序列和，想想怎么办？
首先，对于第一段，没有上一个状态第(0)段，也就是说，它是独立于自己的!
那么方法就是选择一个 (temp) ，然后遍历数组(a),让(temp + a[i])当然(temp)最开始是(0)状态显然，因为还没拿,

当(temp < 0)时那么(temp)就置为(0),因为如果(temp)小于(0),就目前的负数状态再拿，怎么也不如放弃之前状态重新拿较好，显然，所以就置为(0)。
当(temp>0)那么每次就记录最大的(temp)，然后继续接着(temp)状态拿，因为(temp >0)绝对比重新拿好，显然，所以就接着这个状态拿了， 如果疑问：当(temp>0)并且接下来拿了一个绝对值小于(temp)的负数(a[i]), 那么不就是亏了？那么我们可以假设我们亏了，然后我们如果亏了，那么一定有更好的状态即我们顺着我们之前的操作往回找，现在当前数是负数，如果我们不拿这个负数，那么直接拿负数下一个数，就相当于从0开始，显然不如从某个正数开始好，那么你说，前面还有更好的某个数超级大，那么我们就往前找，如果负数前面的数是正数，那么显然拿了好，如果是负数，那么还是得继续找。所以只要不是在(temp)为负数的情况下拿，那么一定是赚的，是有可能对答案造成贡献的。

#include <iostream>
#include <cstring>
using namespace std;
const int N = 2000009; 
int a[N],dp[N],pre[N];
int main() {
    int m, n;
    int temp;
    while (~scanf("%d%d",&m,&n)) {
        for (int i = 1; i<= n; i++)scanf("%d",&a[i]);
        memset(dp, 0, sizeof dp);
        memset(pre, 0, sizeof pre);
        int temp;
        for (int k = 1; k <= m; k++) {
             temp = -0x7fffffff+1;
            for (int i = k; i <= n; i++) {
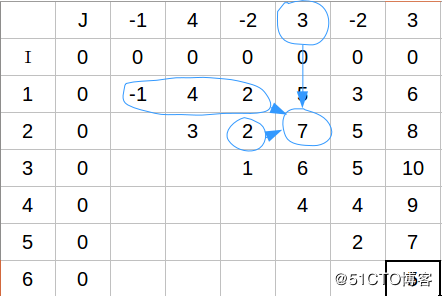
                dp[i] = max(dp[i-1], pre[i-1]) + a[i];
                pre[i-1] = temp;
                temp = max(temp, dp[i]);
            }
        }
        printf("%d
",temp);
    }
}