线性表是什么样子呢?
类似这种,可以当作生活中流水线作业是一样的。
线性表是由n(N>=0)个数据元素(结点)比如a1,a2,a3....an组成的有限序列
数据元素的个数n定义为表的长度,
当n=0时为空表(null)
当n>0时为非空表 L=(a1....an)
a1称为起始点 ,an为终端结点。
对任意一堆相邻结点ai和ai+1 (1<i<n) ai是ai+1的直接前驱,ai+1是ai的直接后继

(图片来源于网络)
如果吧线性表当作火车就更加明显了,火车只有一个火车头(起始节点)一个车尾(终端结点)
火车头(起始节点)前面没有车厢(直接前驱) 但是后面又一节车厢 (直接后继),车尾(终端结点)后面没有多余的车尾(直接后继) ,但是车尾的前面有一节车厢(直接前驱)。
综上可以了解出每一个结点且都有一个直接前驱和一个直接后继
线性表的逻辑结构特征
对于非空的线性表:线性表中结点具有一对一的关系(具体可以看上面的火车例子)
1)线性表中有且仅有一个其实结点a1,没有直接前驱,有且仅有一个直接后继a2;
2)有且仅有一个终端结点an,没有直接后继,有些仅有一个直接前驱an-1;
3)其余的内部结点ai(a<=i<=n-1)都有且仅有一个直接前驱ai-1和一个直接后继ai+1;
线性表的基本运算
初始化 Initiate 秋表长度Length 取表元 get 定位 Locate 插入Insert 删除Delete
线性表顺序存储的方法是:将表中的结点依次存放在计算机内存中一组连续的存储单元中,数据元素在线性表中的邻接关系决定它们在存储空间中的存储位置,即逻辑结构中相邻的结点其存储位置也相邻。
用顺序存储实现的线性表称为顺序表。一般使用数组来表示顺序表。
假定有一组数据,数据间有顺序:13 4 5 15 9 53 24 50 88 42 11
此处数据间的顺序即表示数据间的逻辑关系即线性关系,这一组数据为线性表:
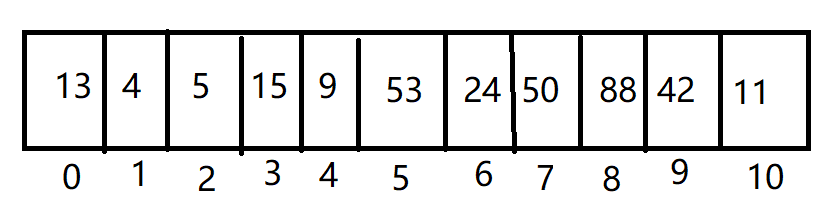
假设已知a1地址为loc(a1),每个数据占c个单元,则计算ai地址
Loc(ai)=Loc(a1)+c*(i-1)
比如 a3 的地址
1 a1=0 2 3 Loc(a3)=a1+(3-1) 4 5 =0+2 6 7 =2
初始化
strudt student{
int ID;//ID
char name[30];//姓名
char sex; //性别
int class;//班级
int age;//年龄
}
student={"01",“zhangsan”,"m","201","20"};
插入
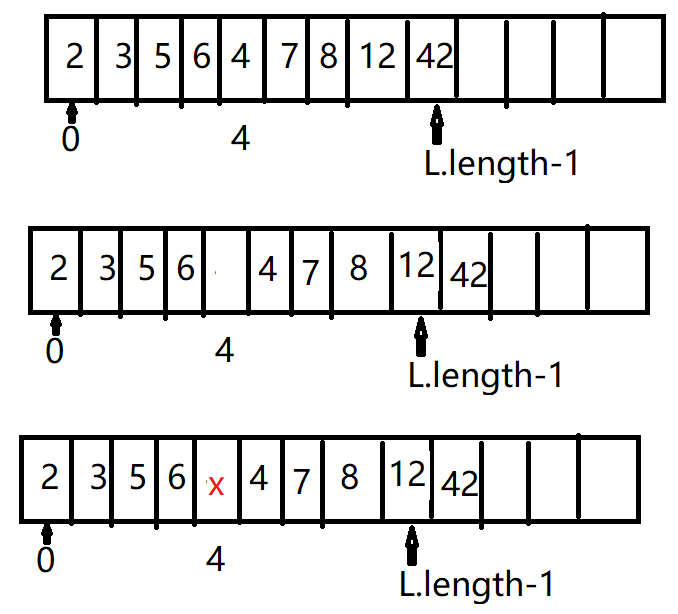
线性表的插入运算是指在表的第i(1<=i<=n+1)个位置上,插入一个新结点x,使长度为n的线性表“:(a1,....ai-1,ai,ai+1,....an)
变成长度为n+1的线性表:
(a1,...ai-1,x,ai,ai+1,....an)
1)当表空间已满,不可在做插入操作
2)当插入位置为非法位置,不可做正常插入操作
void InsertSeqlist (SeqList l,dataType x,int i){ if (l.length==Maxsize)exit("表已满"); if(i<1||l.length+1) exit (”位置错误“);//插入位置是否正确 for(j=l.length;j>=i;j--){//初始化i=l.length l.data[j]=l.data[j-1];//依次后移 l.data[i-1]=x;//元素x置入到下标为i-1的位置 l.length++;}//表长度加1
假设线性表中含有n个数据元素,
在进行插入操作时,有 n+1个位置可插入
在每个位置插入数据的概率是:1/(n+1)
在i位置插入时,要移动n-i+1 个数据
平均时间复杂度为O(n)
删除
线性表的删除运算是指将表的i的结点删去,使长度为n的线性表长度”减一“
当要删除元素的位置I不在表长范围内(即i<1或i->length)时,为非法位置,不能做正常的删除操作
操作过程:
1,若i=n,则只要删除终端结点,无需移动结点;
2,若1<=i<=n-1,则必须将表中位置i+1,i+2,,,,,n的结点,依次前移到位置I
3,该表长度减1
void DeleteSeqList(SeqList L,int i) {
//删除线性表L中的第i个数据结点
if(i<1 || i>L.length) //检查位置是否合法
exit(“非法位置”);
for(j=i;j<L.length;j ++) //第i个元素的下标为i-1
L.data[j-1]=L.data[j]; //依次左移
L.length--; //表长度减1
}
删除算法的分析
假设线性表中含有n个数据元素,
在进行删除操作时,有 n位置可删除
在每个位置删除数据的概率是:1/n
在i位置删除时,要移动 n-i+1个数据
假定在n个位置上删除元素的可能性均等,
平均时间复杂度为O(n)顺序存储结构表示的线性表,在做插入或删除操作时,平均需要移动大约一半的数据元素。
当线性表的数据元素量较大,并且经常要对其做插入或删除操作时,这一点需要值得考虑
定位(查找)
定位运算LocateSeqlist(L,X)的功能是
求L中值等于X的结点序号的最小值,
当不存在这种结点时结果为0 从第一个元素 a1 起依次和x比较,直到找到一个与x相等的数据元素,则返回它在顺序表中的存储下标或序号;或者查遍整个表都没有找到与 x 相等的元素,返回0
int LocateSeqlist(SeqList L, DataType x)
{
int i=0;
while ((i<L. length) && (L.data[i]!=x) ) //在顺序表中查找值为 x 的结点
i++;
if(i<L.length) return i+1; //若找到值为x的元素,返回元素的序号
else return 0; //未查找到值为x的元素,返回0
}
//顺序表的求表长操作,直接输出L.length即可
(1)设表的长度length=n,在插入算法中,元素的移动次数不仅与顺序表的长度
n有关, 还与插入的位置i有关。 插入算法在最坏情况下,其时间复杂度为O(n)。
一般情况下元素比较和移动的次数为n-i+1次,插入算法的平均移动次数约为n/2,
其时间复杂度是O(n)。
(2)删除算法DeleteSeqlist,可得其在最坏情况下元素移动次数为n-1,时间复杂
度为O(n),元素平均移动次数约为(n-1) /2,时间复杂度为O(n)。
(3)对于定位算法,需要扫描顺序表中的元素。以参数x与表中结点值的比较为
标准操作,平均时间复杂度为O(n)。求表长和读表元素算法的时间复杂度为O(1),
就阶数而言,己达到最低
顺序表的优点:
无需为表示结点间的逻辑关系而增加额外存储空间
可以方便地随机存取表中的任一结点
顺序表的缺点:
• 插入和删除运算不方便,必须移动大量的结点
• 顺序表要求占用连续的空间,存储分配只能预先进
行,因此当表长变化较大时,难以确定合适的存储
规模