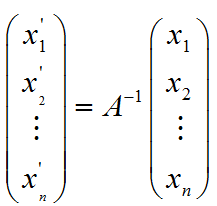设V是数域F上的n维线性空间,ei(i=1,,2,...,n)是基,那么对于任意一个向量a,可表示为a=a1e1+a2e2+...+anen,称有序数组a1,a2...an为向量a在基ei下的坐标。可以看到坐标的定义:ai在xxx基下的坐标。基与坐标分别是严格有序的向量组和数组。
(1)某些向量组线性相关=>其对应的坐标线性相关
(2)假设这两个基之间的线性关系时,基变换
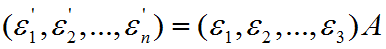
(3)设同一个向量在不同的基下
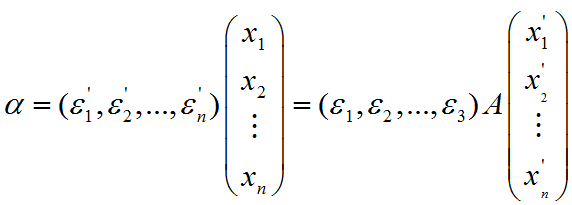
于是,坐标变换为
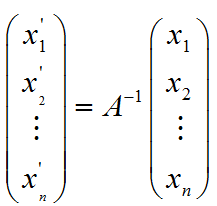
设V是数域F上的n维线性空间,ei(i=1,,2,...,n)是基,那么对于任意一个向量a,可表示为a=a1e1+a2e2+...+anen,称有序数组a1,a2...an为向量a在基ei下的坐标。可以看到坐标的定义:ai在xxx基下的坐标。基与坐标分别是严格有序的向量组和数组。
(1)某些向量组线性相关=>其对应的坐标线性相关
(2)假设这两个基之间的线性关系时,基变换
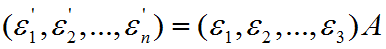
(3)设同一个向量在不同的基下
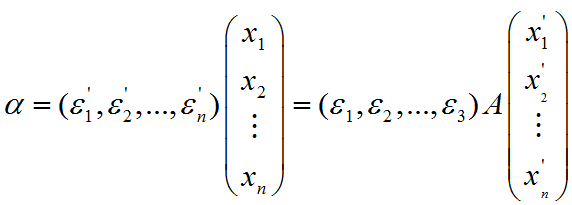
于是,坐标变换为