Poj1915 Knight Moves

试题描述

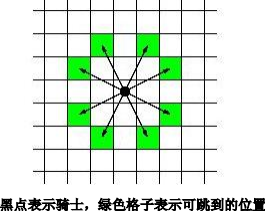
佳佳是一名出色的棋手，声称没有人能像他那样快速地把骑士从一个位置移到另一个位置，你能打败他吗？

编写一个程序，计算一个骑士从棋盘上的一个格子到另一个格子所需的最小步数。骑士一步可以移动到的位置由下图给出。

输入

第一行给出骑士的数量 n。对于每一个骑士都有3行，第一行一个整数 L 表示棋盘的大小（4≤L≤300），整个棋盘大小为 L×L；
第二行和第三行分别包含一对整数 (x,y)，表示骑士的起始点和终点。假设对于每一个骑士，起始点和终点均合理。

输出

对每一个骑士输出一行，一个整数表示需要移动的最小步数。如果起始点和终点相同，则输出 0。

输入示例

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1

输出示例

5
28
0

---

异常SB的写了DFS后来发现算错了复杂度，mdzz

然后BFS发现忘记了条件，然后跳了一个世纪

其实根本不用优化

胡搞BFS就行了

下面给出代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
inline int rd(){
    int x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return x*f;
}
inline void write(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
    return ;
}
int n;
struct node{
    int a,b,num;
}q[100006];
int book[306][306];
int e1,e2,ans;
int l,r;
inline void solve(int x,int y,int z){
    if(!book[x+2][y+1]&&x+2<=n&&y+1<=n) q[++r].a=x+2,q[r].b=y+1,q[r].num=z+1,book[x+2][y+1]=1;
    if(!book[x+2][y-1]&&x+2<=n&&y-1>=0) q[++r].a=x+2,q[r].b=y-1,q[r].num=z+1,book[x+2][y-1]=1;
    if(!book[x-2][y+1]&&x-2>=0&&y+1<=n) q[++r].a=x-2,q[r].b=y+1,q[r].num=z+1,book[x-2][y+1]=1;
    if(!book[x-2][y-1]&&x-2>=0&&y-1>=0) q[++r].a=x-2,q[r].b=y-1,q[r].num=z+1,book[x-2][y-1]=1;
    if(!book[x+1][y+2]&&x+1<=n&&y+2<=n) q[++r].a=x+1,q[r].b=y+2,q[r].num=z+1,book[x+1][y+2]=1;
    if(!book[x-1][y+2]&&x-1>=0&&y+2<=n) q[++r].a=x-1,q[r].b=y+2,q[r].num=z+1,book[x-1][y+2]=1;
    if(!book[x+1][y-2]&&x+1<=n&&y-2>=0) q[++r].a=x+1,q[r].b=y-2,q[r].num=z+1,book[x+1][y-2]=1;
    if(!book[x-1][y-2]&&x-1>=0&&y-2>=0) q[++r].a=x-1,q[r].b=y-2,q[r].num=z+1,book[x-1][y-2]=1;
    return ;
}
inline void bfs(int xx,int yy){
    l=0,r=0;
    q[++r].a=xx,q[r].b=yy,q[r].num=0;
    book[xx][yy]=1;
    while(l<r){
        int x=q[++l].a,y=q[l].b,z=q[l].num;
        if(x==e1&&y==e2){
            ans=z;
            break;
        }
        solve(x,y,z);
    }
    return ;
}
int main(){
    int T=rd();
    while(T--){
        memset(book,0,sizeof(book));
        ans=0;
        n=rd();
        int s1=rd(),s2=rd();
        e1=rd(),e2=rd();
        bfs(s1,s2);
        printf("%d
",ans);
    }
    return 0;
}