DFS与DP算法

名词解释：

DFS(Dynamic Plan)：动态规划

DFS(Depth First Search)：深度优先搜索

DFS与DP的关系

很多情况下，dfs和dp两种解题方法的思路都是很相似的，这两种算法在一定程度上是可以互相转化的。

想到dfs也就常常会想到dp，当然在一些特定的适用场合下除外。

dp主要运用了预处理的思想，而dfs则是类似于白手起家，一步步探索。一般来讲，能够预处理要好些，好比战争前做好准备。

dfs和dp都是十分重要的基础算法，在各个竞赛中都有涉及，务必精通。

---

题目：

The Triangle

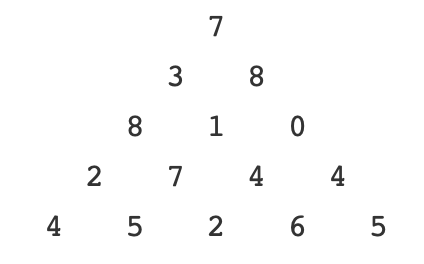
描述：

编写一个程序，计算从顶部开始到底部某处的路径上传递的最大数字总和。 每个步骤可以向左下或右下滑动。

输入：

程序是从标准输入读取。 第一行包含一个整数N：三角形中的行数。 以下N行描述了三角形的数据。 三角形中的行数1<N<=100.三角形中的数字全部为整数，介于0到99之间。

输出：

程序是标准输出。输出最大的整数和。

 样例：

输入：

输出：

---

DFS思路：

自顶向下，将每种路径都走一遍。

通过迭代计算到最后一层，记录最后一层的所有值。最后一层中的最大值即为所求。

具体代码：

#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
using namespace std;

// the maximum of the triangle ordinal
const int max_ordinal = 100;
// the depth
int num_of_rows;
// save data
int data[max_ordinal][max_ordinal];
// save the data of the final level
vector<int> ans;

void dfs(int level, int sum, int column)
{
  // avoid multi calculate
  int current_sum = sum+data[level][column];
  // save data which was in final level
  if(level+1 == num_of_rows)
  {
    ans.push_back(current_sum);
    return;
  }
  // binary tree
  dfs(level+1, current_sum, column);
  dfs(level+1, current_sum, column+1);
}

int main()
{
  cin >> num_of_rows;
  for(int i = 0; i < num_of_rows; i++)
    for(int j = 0; j <= i; j++)
      scanf("%d", &data[i][j]);

  dfs(0, 0, 0);
  cout << "output data:" << endl;

  sort(ans.begin(), ans.end(), greater<int>());
  for(int i = 0; i < ans.size(); i++)
  {
    cout << ans[i] << "	";
    if(!((i+1) % 5)) cout << endl;
  }
  cout << endl;

  return 0;
}

---

DP思路：

dfs的思路是从上到下，而dp的思路是：从第二层开始，每下去一次往回看一下并取上一层相邻两个大的那个。

具体代码：

#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;

// same as DFS
const int max_ordinal = 100;
int num_of_rows;
int data[max_ordinal][max_ordinal];
// the array of the dp method
int dp[max_ordinal][max_ordinal];

int main()
{
    cin >> num_of_rows;
    for(int i = 0; i < num_of_rows; i++)
        for(int j = 0; j<= i; j++)
            scanf("%d", &data[i][j]);

    // dp now
    dp[0][0] = data[0][0];
    for(int i = 1; i < num_of_rows; i++)
    {
        for(int j = 0; j <= i; j++)
        {
            if(j-1 >= 0)
            {
                dp[i][j] = data[i][j] + max(dp[i-1][j], dp[i-1][j-1]);
            } else {
                dp[i][j] = data[i][j] + dp[i-1][j];
            }
        }
    }

  // calling 'sort' method
    sort(dp[num_of_rows-1], &dp[num_of_rows-1][num_of_rows], greater<int>());
    for(int i = 0; i < num_of_rows; i++)
        cout << dp[num_of_rows-1][i] << " ";
    cout << endl;
    cout << "answer is: ";
    cout << dp[num_of_rows-1][0] << endl;

    return 0;
}