组合数学
定义
实际上是 不可重复组合排列 。一般用C来表示。由于所用到的知识甚微,故不需要什么高深的解释。
公式
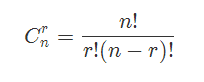
其意义是 从n中取r个,所有的情况数
n!意味着阶乘。实现起来就是 ans=1*2*2*4*...*n
数学期望
定义
何老板的PPT实在是太棒了,所以我决定引一张!!!

也就是说,累加事件*概率所得到的结果,就是要求的数学期望!
入门性应用
数学期望能解决什么问题呢?

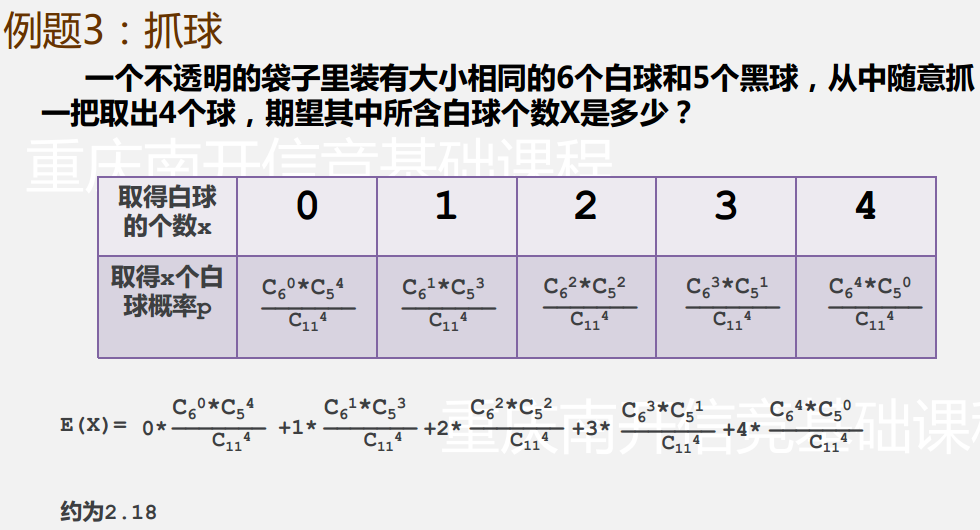

这个题提出了一个思想:计算单体贡献。也就是每张卡对s1+...+st的贡献。
相关性质
x是线性关系的随机变量 k=a*x+b的数学期望,有
E(a*x+b)=a*E(x)+b
对于任意随机变量x和y以及常量a和b,有
E(a*x+b*y)=a*E(x)+b*E(y)
当两个随机变量x和y独立
E(x*y)=E(x)*E(y)
题目中的ShowTime
吸血鬼 NKOJ2126

题解直接写到代码里了
#include<iostream> using namespace std; double f[100100]; int n; const double U=1.00; double p; //B H K double C(int up,int down){ double ans; double uper=1; double downer=1; double ano=1; for(int i=2;i<=up;i++){ uper*=i; } for(int i=2;i<=down;i++){ downer*=i; } for(int i=2;i<=down-up;i++){ ano*=i; } ans=downer/(uper*ano); return ans; } int main(){ cin>>n>>p; f[n]=0; //F[i]表示已经有i只鬼,仍需期望F[i]天 //对于每一天,只有两种状态。即新增一鬼和鬼数不变 //对于新增,F[i+1] //对于不变,F[i] //F[i+1]的概率为 p1= Cn-i 1* Ci 1/Cn 2 * p //F[i]的概率为 p2=1-p1 //F[i]=F[i+1]*p1+F[i]*p2+1 // f[i]=f[i+1]+1/p1 for(int i=n-1;i>=1;i--){ double Index=C(1,n-i)*C(1,i)/C(2,n)*p; //cout<<U/Index<<endl; f[i]=f[i+1]+(double)(U/Index); } printf("%.3f",f[1]); }