机电传动控制第二周读书笔记

教材阅读

一．直流电机的基本工作原理

直流电机可做发电机和电动机运行，不同之处在于直流电机电刷间的电动势E与电流的方向相同或相反的。

直流电机电刷间的电动势

E=K_eΦn

直流电机的电磁转矩

T=K_tΦI_a

 

电机在不同运行方式下E和T的作用

电机运行方式	E与的方向	E的作用	T的性质	转矩之间的关系
发电机	相同	电源电动势	阻转矩	T1=T+TL
电动机	相反	反电动势	驱动转矩	T=TL+T0

其中，T₁-原动机转矩

         T_L-负载转矩

 

二．直流发电机

1. 他励发电机

发电机端电压与电流关系式

U=E-I_aR_a

I_a=(E-U)/R_a

I_a=I

I=U/R

发电机空载时，I_a=0，空载电压

U₀=E=K_eΦn

空载特性曲线：E-I_f曲线，表明可利用改变励磁电流的方法来获得所需的电压。他励发电机空载特性见图3.9。
外特性曲线： U-I曲线，转速n和励磁电流为常数时发电机端电压U与负载电流I关系的曲线。他励发电机外特性见图3.10。从空载到满载（额定负载）电压的变化率为（一般为5%~10%）

 

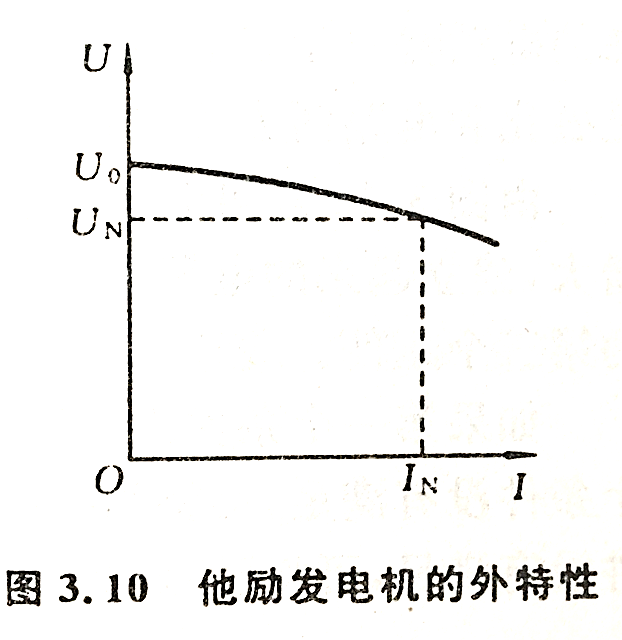
2.并励发电机

发电机端电压与电流关系式

U=E-I_aR_a

I_a=(E-U)/R_a

I_f=U/R_a

I=U/R

I_a=I+I_f≈I

并励发电机空载特性见图3.12。

并励发电机外特性见图3.13。

3. 复励发电机

 

三．直流电动机的机械特性

1. 他励直流电动机

电枢回路的电压平衡方程

U=E+I_aR_a

带入E=K_eΦn得

n=U/(K_eΦ)-R_aI_a/(K_eΦ)

带入I_a=T/(K_tΦ)得

n=U/(K_eΦ)-R_aT/(K_eK_tΦ²) =n₀-Δn

机械特性曲线：n-T曲线。他励电动机的机械特性见图3.16。

理想空载转速

n₀=U/(K_eΦ)

机械特性硬度

β=dT/dn=ΔT/Δn×100%

（绝对硬特性：β→∞ 硬特性：β>10 软特性：β<10）

(1)固有机械特性

固有机械特性：自然特性，指额定条件下的n=f(T)曲线。

此时U=U_N、Φ=Φ_N，n=f(T)曲线是一条直线。

(2)人为机械特性

人为机械特性：指供电电压U或磁通Φ不是额定值、电枢电路串接附加电阻R_ad时的机械特性。

a. 电枢电路中串接附加电阻时的认为机械特性

当U=U_N、Φ=Φ_N、电枢电路中串接附加电阻R_ad时，此时R_a=R_ad+R_a，则

n=U_N/(K_eΦ_N)-(R_ad+R_a)T/(K_eK_tΦ_N²) =n₀-Δn

b. 改变电枢电压U时的人为机械特性

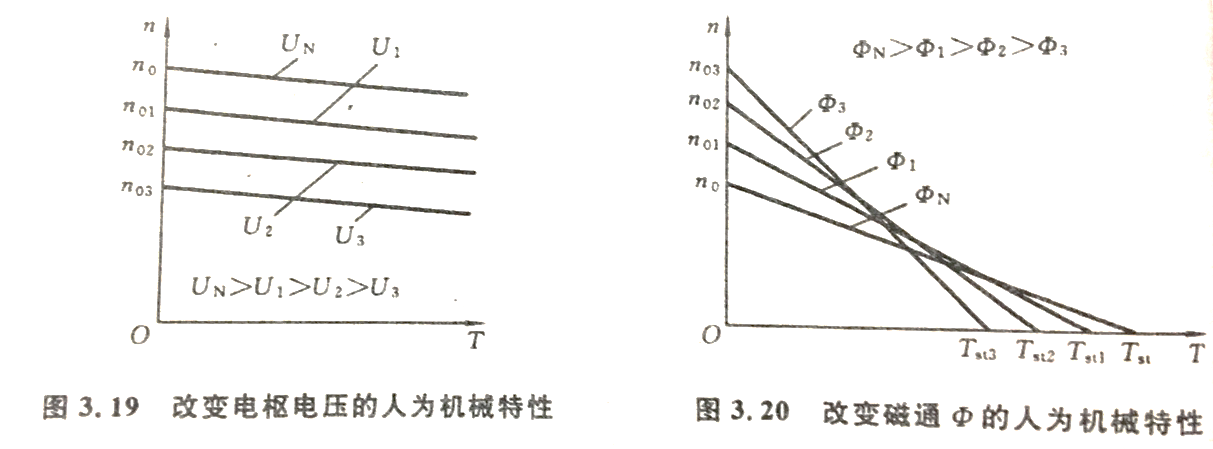
当Φ=Φ_N、R_ad=0而改变电枢电压U时，n₀=U/(K_eΦ_N)随U改变而改变，但Δn不变。如图3.19。

c. 改变磁通Φ时的人为机械特性

当U=UN、Rad=0而改变磁通Φ时，n₀=U_N/(K_eΦ)和Δn=RaT/(K_eK_tΦ²)随Φ改变而改变。如图3.20。

飞车：I_f=0时，由于定子还有比较小的剩磁，剩磁产生的启动转矩很小（T=K_tΦn），理想的空载转速很大（n₀=U/(K_eΦ)），机械特性曲线很陡，空载时转速超出机械强度允许的值。

堵转：负载转矩大于电磁转矩（T_L>T）时，电机不能启动，即n=0，E=K_eΦn=0，此时I_st=U/R_a（短路电流）远远超过额定值。

2. 串励直流电动机

3. 复励直流电动机

四．他励直流电动机

1. 启动特性

2. 调速特性

3. 制动特性

 

《自动化技术中的进给电气传动》1.3节

一．  微分方程

 

I: U_A-e_M=i_AR_A+L·di_A/dt

II: M_M=c_Mi_A

III: M_M-M_L=J_Ges·dω_M/dt

IV: e_M=c_Mω_M

（c_M是电动机常数，与K_T和K_E值相同）

整理上述方程可得

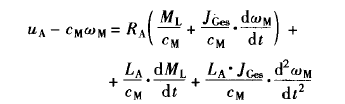
引入电气时间常数T_elA=L_A/R_A，则

定标：引入电动机空载时最大角速度ω_maxM，空载时电枢最大电压U_maxA=E_maxM=c_Mω_maxM，转轴堵转时的最大转矩，即短路转矩M_stA=I_maxAc_M=U_maxAc_M/R_A=ω_maxMc_M²/R_A

通过方程两边同乘R_A/U_maxA，将定标量带入方程得

引入机械时间常数T_mechA=J_Gesω_maxM/M_stA=J_GesR_A/c_M²得

以ω_M作输出量，u_A和M_L作输入量，假定M_L=0，该微分方程与P-T₂环节的微分方程相同，即不可调传动系统在基准响应特性如同P-T₂环节一样，其中

特征值T_A^*=√(T_elAT_mechA)

阻尼因数D_A^*=1/2√(T_mechA/T_elA)

干扰响应特性，保持u_A恒定，并使M_L呈阶跃式变化

二．  阶跃响应特性

阶跃响应特性用来描述一个传递环节或一个系统的输出量在输入量发生一次阶跃式变化时随时间变化过程

 

《控制系统设计指南》第1章和第2章

一. 控制理论

控制器

 

被控机器：被控对象与反馈装置

二. 频率域研究法 

1. 拉普拉斯变换

F(s)=∫₀^∞f(t)e^-stdt

2. 传递函数

拉普拉斯算子

s=σ+jω

s_稳态=j2∏f

均一性：设输入r(t)产生输出c(t)，则kr(t)的输出为kc(t)

叠加性：设输入r₁(t)产生输出c₁(t)，输入r₂(t)产生输出c₂(t)，则r₁(t)+r₂(t)的输出为c₁(t)+c₂(t)

时不变性：设输入r(t)产生输出c(t)，则r(τ-t)的输出为c(τ-t)

3. 传递函数举例

(1) 积分与微分

积分算子1/s，微分算子s

(2) 滤波器

(3) 补偿器

(4) 延迟

一个T秒的延迟在时间域定义为

c(t)=r(t-T)

其相应的频率域描述为

T_延迟(s)=e^-st

物理元件的传递函数

反馈的传递函数：理想情况下反馈装置的传递函数为1

4. 框图

(1) 组合框

a. 串联框

b. 反馈电路的简化

(2) Mason信号流图

a. 找出回路

b. 找出控制回路的行列式

c. 找到所有的前向路径

d. 找出每条前向路径的余因子

e. 建立传递函数

5. 相位增益

(1) 相位与增益

增益=20×lg(出幅/入幅)

相位=-360×F×t_DELTA (F-频率，t_DELTA-延迟时间)

(2) Bode图

6. 性能测量

(1) 指令响应

(2) 稳定性

(3) 与频率域对应的时间域