TSP 模拟退火

TSP——模拟退火解法

都知道TSP是经典的NP问题，从一个点开始遍历所有点，不重复，求最短路径。

可以用枚举终点，跑流量为2的最小费用，图论来做，时间复杂度为 ​ 费用流已经用到堆优化了。显然点，边较多将无法承受。

如果不要求精确解，使用模拟退火也是一个不错的选择。模型简单，转移很暴力。

先随机生成一些解，然后随机挑两个点，开始试探转移。

 

这里，几乎是按照退火算法模板写的了，有初始化，有状态转移，有接受准则。

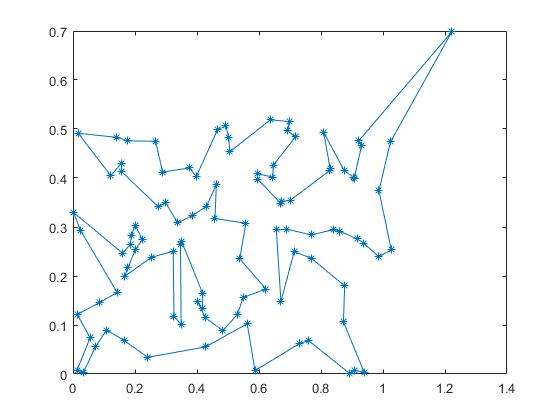
clc, clear
sj0=load('sj.txt');
x=sj0(:,[1:2:8]);x=x(:);
y=sj0(:,[2:2:8]);y=y(:);
sj=[x y]; d1=[70,40]; 
sj=[d1;sj;d1]; sj=sj*pi/180;
d=zeros(102);
for i=1:101
   for j=i+1:102
    d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
   end
end
d=d+d';
path=[];long=inf;
​
rand('state',sum(clock));  %初始化随机数发生器
​
for j=1:1000  %求较好的初始解
    path0=[1 1+randperm(100),102]; temp=0;
    for i=1:101
        temp=temp+d(path0(i),path0(i+1));
    end
    if temp<long
        path=path0; long=temp;
    end
end
​
e = 0.1^30;
L = 20000;
at = 0.999;
T = 1;
​
for k = 1:L
    c = 2+floor(100*rand(1,2));
    c = sort(c);
    c1 = c(1);
    c2 = c(2);
    
    df=d(path(c1-1),path(c2))+d(path(c1),path(c2+1))-d(path(c1-1),path(c1))-d(path(c2),path(c2+1));
    
    if df < 0 
        path=[path(1:c1-1),path(c2:-1:c1),path(c2+1:102)]; 
        long = long+df;
    elseif exp(-df/T)>rand
        path=[path(1:c1-1),path(c2:-1:c1),path(c2+1:102)]; 
        long=long+df;
    end
    
    T = T*at;
    if T < e
        break;
    end
end
​
xx = sj(path,1);
yy = sj(path,2);
plot(xx,yy,'-*');