http://www.51nod.com/Challenge/Problem.html#problemId=1213
原理:
每个点在以它为顶点的45°角范围内,只可能连向距离(曼哈顿距离)它最近的点。
证明:
以点A为原点,y轴正半轴向x轴正半轴方向偏45°角为例:
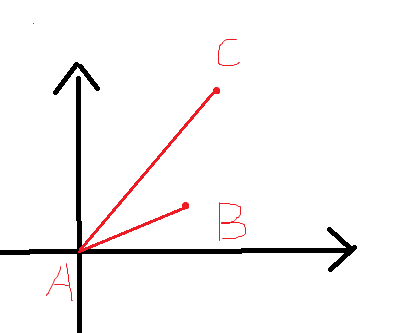
如图所示,设|AB|<=|AC| (所有距离都是曼哈顿距离)
A(0,0) B(x1,y1) C(x2,y2)
|AB|=x1+y1 |AC|=x2+y2 |BC|=|x2-x1|+|y2-y1|
即 x1+y1<= x2+y2
如果能够证明 |BC|<=|AC| ,即|x2-x1|+|y2-y1|<= x2+y2
那么对于ABC三点,只需要A向B连边即可。因为对C来说,至少与B连边比与A连边更优。
根据x1 y1 x2 y2大小分情况讨论:
①x1<=x2 y1<=y2 ,此时 |AB|+|BC|=|AC|,即x1+y1+|x2-x1|+|y2-y1|=x2+y2
所以|x2-x1|+|y2-y1|=x2+y2-(x1+y1)< x2+y2
②x1<=x2 y1>y2 ,此时|BC|=x2-x1+y1-y2,|AC|-|BC|=x2+y2-(x2-x1+y1-y2)=x1-y1+y2*2
假设|AC|<|BC|,则x1-y1+y2*2<0,即y1>x1+y2*2
那么|AB|=x1+y1>2*x1+2*y2 |AC|=x2+y2<=2*y2<|AB|,与最初的假设|AB|<=|AC| 不符
所以|AC|>=|BC|
③x1>x2 y1<=y2 ,此时|BC|=x1-x2+y2-y1,|AC|-|BC|=x2+y2-(x1-x2+y2-y1)=y1-x1+x2*2
∵ x1>x2 且 x1+y1<= x2+y2,∴ y1<y2
∵ B在A的y轴正半轴向右偏45°角范围内 ∴y1>=x1
∴ x1<=y1<y2
∴y1-x1+x2*2>0
∴ |AC|>|BC|
④x1>x2 y1>y2 不满足|AB|<=|AC| 的假设,不存在
一共有8个45°方向,因为克鲁斯卡尔算法相当于使用双向边,所以是4个方向,利用坐标变换到上面的方向即可
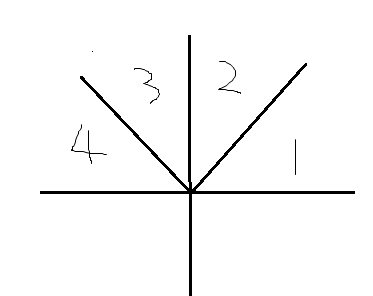
原本寻找的是区域2的点
把所有的点交换x和y坐标,就统计到了 区域1的点(1 2交换 3 4交换)
再把x坐标变为相反数,就统计到了区域4的点(1 4再交换 2 3再交换)
最后再交换x和y坐标,就统计到了区域3的点(1 2再交换 3 4再交换)
具体实现:
对于每个点(x0,y0),我们要寻找以它为顶点,以y轴正半轴向右45°角范围内,距离他最近的点
即满足以下两个条件:
1. x>=x0
2. y-x>=y0-x0
并且x+y-(x0+y0)最小的点
即满足上述2个条件并且x+y最小的 点(x,y)
采用线段树或者树状数组维护最小值
条件1将点按x坐标为第一关键字,y左边按第二关键字,从大到小排序,依次插入树状数组或者是线段树。这样每次查询的时候,在树中的点都是满足条件1的点
条件2 每次查询一个点完毕后,在该点的y-x位置处,用该点的x+y更新
查询满足条件的最小的x+y:在大于等于当前点的y-x的区间里,查询最小值
然后y-x要离散化
小细节:
因为树状数组更方便查询前缀情况,所以可以是离散化x-y,就变成在小于等于x-y的区间里查询最小值
#include<cstdio> #include<iostream> #include<algorithm> #define N 50001 #define lowbit(x) x&-x using namespace std; int xx[N],yy[N]; struct node { int x,y,xy,id; }e[N]; int has[N]; int mi[N],who[N]; int tot; struct edge { int u,v,w; }f[N<<2]; int fa[N]; bool cmp1(node p,node q) { if(p.x!=q.x) return p.x>q.x; return p.y>q.y; } bool cmp2(edge p,edge q) { return p.w<q.w; } int find(int i) { return fa[i]==i ? i : fa[i]=find(fa[i]); } int getmin(int x) { int mii=2e9; int whoo=-1; while(x) { if(mi[x]<mii) { mii=mi[x]; whoo=who[x]; } x-=lowbit(x); } return whoo; } void change(int x,int val,int to,int n) { while(x<=n) { if(val<mi[x]) { mi[x]=val; who[x]=to; } x+=lowbit(x); } } int main() { int n; scanf("%d",&n); for(int i=1;i<=n;++i) { scanf("%d%d",&xx[i],&yy[i]); e[i].x=xx[i]; e[i].y=yy[i]; } for(int i=1;i<=n;++i) e[i].id=i; int p; for(int k=1;k<=4;++k) { if(k==2) for(int i=1;i<=n;++i) swap(e[i].x,e[i].y); if(k==3) for(int i=1;i<=n;++i) e[i].x=-e[i].x; if(k==4) for(int i=1;i<=n;++i) swap(e[i].x,e[i].y); sort(e+1,e+n+1,cmp1); for(int i=1;i<=n;++i) has[i]=e[i].x-e[i].y; sort(has+1,has+n+1); int m=unique(has+1,has+n+1)-has-1; for(int i=1;i<=n;++i) e[i].xy=lower_bound(has+1,has+m+1,e[i].x-e[i].y)-has; for(int i=1;i<=m;++i) mi[i]=2e9; for(int i=1;i<=n;++i) { p=getmin(e[i].xy); if(p!=-1) { f[++tot].u=e[i].id; f[tot].v=p; f[tot].w=abs(xx[e[i].id]-xx[p])+abs(yy[e[i].id]-yy[p]); } change(e[i].xy,e[i].x+e[i].y,e[i].id,m); } } sort(f+1,f+tot+1,cmp2); int now=0,fu,fv; for(int i=1;i<=n;++i) fa[i]=i; long long ans=0; for(int i=1;i<=tot;++i) { fu=find(f[i].u); fv=find(f[i].v); if(fu!=fv) { ans+=f[i].w; fa[fu]=fv; } } printf("%lld",ans); }