A.Digits Sequence Dividing
题意:给你一个1-9的数字字符串,把它划分成若干段(>=2)段,使其大小递增。
错误:当长度为2的时候没考虑

#include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> #include<algorithm> #include<iostream> #include<map> using namespace std; typedef long long ll; const int p=998244353; int n,q; char s[1010]; int main() { scanf("%d",&q); for(int i=1;i<=q;i++) { scanf("%d",&n); scanf("%s",s); if(s[0]<s[1]||n>2) { printf("YES "); printf("2 "); printf("%c ",s[0]); for(int j=1;j<n;j++) printf("%c",s[j]); printf(" "); } else{ printf("NO "); } } }
B.Digital root
题意:求第k大的数根为x的数

#include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> #include<algorithm> #include<iostream> #include<map> using namespace std; typedef long long ll; const int p=998244353; int n,q; ll k,x; char s[1010]; int main() { scanf("%d",&q); for(int i=1;i<=q;i++) { scanf("%I64d%I64d",&k,&x); printf("%I64d ",(k-1)*9+x); } }
C.Brutality
题意:给你两个序列,第一个为价值,第二个为种类,求价值最大(一个限制条件是在种类相同的段里不能选超过k个)
思路:对个每个小段快排,取前k大。

#include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> #include<algorithm> #include<iostream> #include<vector> #include<map> using namespace std; typedef long long ll; const int p=998244353; int n,k,a[201010],q[201000]; char s[201000]; ll ans; vector<int> mp[30]; bool cmp(int a,int b) { return a>b; } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); } scanf("%s",s+1); int w=1,flag=s[1];q[1]=a[1]; for(int i=2;i<=n;i++) { if(s[i]!=flag) { sort(q+1,q+1+w,cmp); for(int j=1;j<=min(w,k);j++) ans+=q[j]; w=1;flag=s[i];q[1]=a[i]; } else{ q[++w]=a[i]; } } sort(q+1,q+1+w,cmp); for(int j=1;j<=min(w,k);j++) ans+=q[j]; // for(int i=1;i<=n;i++) // { // mp[s[i]-97].push_back(a[i]); // } // for(int i=0;i<=29;i++) // sort(mp[i].begin(),mp[i].end()); // for(int i=0;i<=29;i++) // { // for(int j=mp[i].size()-1;j>=0;j--) // { // ans+=mp[i][j]; // printf("%I64d %d ",ans,mp[i].size()); // if(mp[i].size()-j+1>k) break; // } // } printf("%I64d ",ans); }
D.Compression
题意:对于一个01矩形找到最大的矩形,使其满足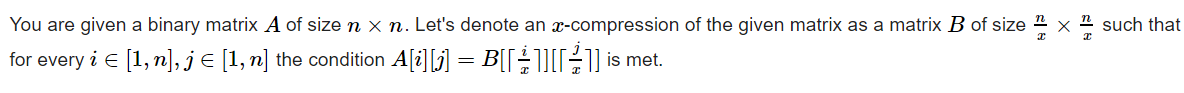
思路1:这道题的题意就是分解成若干最大的矩形是,使其内的值都为0或者1。用sum[i][j]表示二维前缀和,时间复杂度O(n*n*π*π/6)

#include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> #include<algorithm> #include<iostream> #include<vector> #include<map> using namespace std; typedef long long ll; const int p=998244353; int n,mp[5210][5210],sum[5210][5210],flag,w[10100]; char s[201010]; bool chec(int x,int y,int k) { //printf("%d %d %d ",x,y,k); int zhi=sum[x*k][y*k]-sum[(x-1)*k][y*k]-sum[x*k][(y-1)*k]+sum[(x-1)*k][(y-1)*k]; //printf("zhi=%d ",zhi); if(zhi==0||zhi==k*k) return 0; return 1; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%s",s); for(int j=0;j<strlen(s);j++) { int x; if(s[j]<='9') x=s[j]-'0'; else x=s[j]-'A'+10; int l=0; while(x>0) { mp[i][4*(j+1)-l]=x%2; x/=2;l++; } } } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+mp[i][j]; } } int l=0; for(int i=1;i<=trunc((double)sqrt(n));i++) if(n%i==0) { w[++l]=i;w[++l]=n/i; } sort(w+1,w+1+l); for(int i=l;i>=1;i--) { flag=0; int kuai=n/w[i]; // printf("%d ",kuai); for(int k=1;k<=kuai;k++) { for(int j=1;j<=kuai;j++) if(chec(k,j,w[i])) { flag=1; // printf(" %d ",w[i]); break; } if(flag) break; } if(!flag) { flag=w[i]; break; } } printf("%d ",flag); }
思路2:巧妙官方题解,对于每一行求连续的1或者0的个数为k,则答案为ans=gcd(ans,k),(ans一开始为n,表示坐到当前能划分的最大的长度)时间复杂度O(n*n),妙哉。

#include <bits/stdc++.h> using namespace std; const int N = 5200; int n; bool a[N][N]; void parse_char(int x, int y, char c) { int num = -1; if (isdigit(c)) { num = c - '0'; } else { num = c - 'A' + 10; } for (int i = 0; i < 4; ++i) { a[x][y + 3 - i] = num & 1; num >>= 1; } } int main() { #ifdef _DEBUG freopen("input.txt", "r", stdin); // freopen("output.txt", "w", stdout); #endif scanf("%d", &n); char buf[N]; for (int i = 0; i < n; ++i) { scanf("%s", buf); for (int j = 0; j < n / 4; ++j) { parse_char(i, j * 4, buf[j]); } } int g = n; for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { int k = j; while (k < n && a[i][k] == a[i][j]) ++k; g = __gcd(g, k - j); j = k - 1; } } for (int j = 0; j < n; ++j) { for (int i = 0; i < n; ++i) { int k = i; while (k < n && a[k][j] == a[i][j]) ++k; g = __gcd(g, k - i); i = k - 1; } } cout << g << endl; return 0; }
思路3:bitset优化,复制出第一行的状态tmp,之后的i+1到i+x都是tmp。最后A数组和B数组比较一下,复杂度为O(n*n*因子个数/64)(code by DUP 4)

#include <bits/stdc++.h> using namespace std; #define N 5510 int n; bitset <N> a[N], b[N], tmp; char s[N][N]; char Hash[210]; int res; void change(int x) { a[x].reset(); for (int i = 1, j = 0; i <= n / 4; ++i) { int num = Hash[s[x][i]]; for (int k = 3; k >= 0; --k) a[x][++j] = (num >> k) & 1; } } /*void solve(int x) { for (int i = 1, ii = 1; i <= n; i += x, ++ii) { for (int j = 1, jj = 1; j <= n; j += x, ++jj) b[ii][jj] = a[i][j]; } for (register int i = 1; i <= n; ++i) for (register int j = 1; j <= n; ++j) //if (a[i][j] != b[i % x == 0 ? i / x : i / x + 1][j % x == 0 ? j / x : j / x + 1]) if (a[i][j] != a[i - ((i - 1) % x)][j - ((j - 1) % x)]) return; res = max(res, x); }*/ bool solve(int x) { for (int i = 1; i <= n; i += x) { tmp.reset(); for (int j = 1; j <= n; j += x) for (int k = j; k < j + x; ++k) tmp[k] = a[i][j]; //printf("%d %d ", x, i); //for (int j = 1; j <= n; ++j) printf("%d", tmp[j] ? 1 : 0); //puts(""); for (int j = i; j < i + x; ++j) { b[j] &= 0; b[j] |= tmp; } } for (int i = 1; i <= n; ++i) if ((a[i] ^ b[i]) != 0) { //puts("bug"); //printf("%d %d ", n, x); //for (int j = 0; j <= 10; ++j) printf("%d", a[i][j] ? 1 : 0); puts(""); //for (int j = 0; j <= 10; ++j) printf("%d", b[i][j] ? 1 : 0); puts(""); return false; } return true; } int main() { for (int i = 0; i <= 9; ++i) Hash[i + '0'] = i; Hash['A'] = 10; Hash['B'] = 11; Hash['C'] = 12; Hash['D'] = 13; Hash['E'] = 14; Hash['F'] = 15; while (scanf("%d", &n) != EOF) { for (int i = 1; i <= n; ++i) scanf("%s", s[i] + 1); for (int i = 1; i <= n; ++i) change(i); /*for (int i = 1; i <= n; ++i) { for (int j = 1; j <= n; ++j) printf("%d", a[i][j] ? 1 : 0); puts(""); }*/ res = 1; vector <int> fac; for (int i = 1; i * i <= n; ++i) if (n % i == 0) fac.push_back(i), fac.push_back(n / i); sort(fac.begin(), fac.end()); fac.erase(unique(fac.begin(), fac.end()), fac.end()); reverse(fac.begin(), fac.end()); for (auto it : fac) { if (solve(it)) { res = it; break; } } printf("%d ", res); } return 0; }
E.Vasya and Binary String
题意:给个长度为n的01字符串s,以及长度为n数组a.你每次可以选择任意长度L的连续子串(要求子串每个字符相同)从原串中去掉,并获得a[L]的值。问你可能获得的值最多是多少
思路:区间DP,F[I][J][K]表示区间i到j后面跟着和S【J】相同的字符个数为K的最大价值
dp[l][r][k]=max(dp[l][r][k],dp[l][r-1][0]+a[k+1]);//去掉第R个字符
dp[i][j][k]=max(dp[i][j][k],dp[i][p][k+1]+dp[p+1][j-1][0]);//将p+1和j-1区间合并
用记忆化搜索简短一些

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int N = 105; LL dp[N][N][N]; string s; int a[N]; LL dfs(int l, int r, int k) { if(l > r) return 0; if(l == r) return a[k+1]; if(~dp[l][r][k]) return dp[l][r][k]; dp[l][r][k] = dfs(l, r-1, 0) + a[k+1]; for (int i = l; i < r; i++) { if(s[i] == s[r]) { dp[l][r][k] = max(dp[l][r][k], dfs(i+1, r-1, 0) + dfs(l, i, k+1)); } } return dp[l][r][k]; } int main() { int n; cin >> n; cin >> s; for (int i = 1; i <= n; ++i) cin >> a[i]; memset(dp, -1,sizeof(dp)); cout << dfs(0, n-1, 0) << endl; return 0; }
F.Vasya and Endless Credits
题意:三个数组A[I],B[I],K[I],表示第i张卡,你可以向银行借A[I]元,之后的K[I]个月你都要向银行还B[I]块钱,一个月只能用一张卡,问你在手中钱的最大值是多少
思路:巧妙的匈牙利算法,构建矩形,使得 mati,j=aj−min(i,kj)⋅bj ,这道题就转化为在这个矩形中挑选一些在不同行不同列的数字是其和最大

#include <bits/stdc++.h> using namespace std; const int N = 505; const long long INF = 1e18; int n; long long a[N][N]; int up[N], down[N], k[N]; long long u[N], v[N]; int p[N], way[N]; int main(){ cin >> n; for(int i = 0; i < n; ++i) cin >> up[i] >> down[i] >> k[i]; for(int i = 0; i < n; ++i) for(int j = 0; j < n; ++j) a[i + 1][j + 1] = -(up[j] - min(i, k[j]) * 1LL * down[j]); long long res = 0; for(int i = 1; i <= n; ++i){ p[0] = i; int j0 = 0; vector<long long> minv (n + 1, INF); vector<char> used (n + 1, false); do{ used[j0] = true; int i0 = p[j0], j1; long long delta = INF; for (int j = 1; j <= n; ++j) if (!used[j]){ long long cur = a[i0][j] - u[i0] - v[j]; if (cur < minv[j]) minv[j] = cur, way[j] = j0; if (minv[j] < delta) delta = minv[j], j1 = j; } for (int j = 0; j <= n; ++j) if (used[j]) u[p[j]] += delta, v[j] -= delta; else minv[j] -= delta; j0 = j1; }while (p[j0] != 0); do { int j1 = way[j0]; p[j0] = p[j1]; j0 = j1; } while (j0); res = max(res, v[0]); } cout << res << endl; return 0; }
G.Vasya and Maximum Profit
题意:给你n道题目,每道题目都有两个属性di和A-ci,你要求最大子段和,∑A-ci +gap(l,r)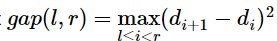
思路:左边的∑A-ci可以用线段树处理,右边的gap(l,r)可以先按照gap(i,i+1)从小到大排序,用set来合并联通的两个段。

#include<bits/stdc++.h> using namespace std; const int N = int(3e5) + 99; struct node{ long long sum, ans, pref, suf; node () {} node(int x){ sum = x; x = max(x, 0); pref = suf = ans = x; } }; node merge(const node &a, const node &b){ node res; res.sum = a.sum + b.sum; res.pref = max(a.pref, a.sum + b.pref); res.suf = max(b.suf, b.sum + a.suf); res.ans = max(max(a.ans, b.ans), a.suf + b.pref); return res; } int n, x; pair<int, int> p[N]; node t[N * 4]; void upd(int v, int l, int r, int pos, int x){ if(r - l == 1){ assert(pos == l); t[v] = node(x); return; } int mid = (l + r) / 2; if(pos < mid) upd(v * 2 + 1, l, mid, pos, x); else upd(v * 2 + 2, mid, r, pos, x); t[v] = merge(t[v * 2 + 1], t[v * 2 + 2]); } node get(int v, int l, int r, int L, int R){ if(L >= R) return node(0); if(l == L && r == R) return t[v]; int mid = (l + r)/ 2; return merge(get(v * 2 + 1, l, mid, L, min(mid, R)), get(v * 2 + 2, mid, r, max(L, mid), R)); } int main() { scanf("%d %d", &n, &x); for(int i = 0; i < n; ++i){ scanf("%d %d", &p[i].first, &p[i].second); p[i].second = x - p[i].second; } sort(p, p + n); for(int i = 0; i < n; ++i) upd(0, 0, n, i, p[i].second); vector <pair<int, int> > v; for(int i = 1; i < n; ++i) v.emplace_back(p[i].first - p[i - 1].first, i); sort(v.begin(), v.end()); long long res = 0; set <pair<int, int> > s; for(int i = 0; i < n; ++i){ s.insert(make_pair(i, i + 1)); res = max(res, 1LL * p[i].second); } int l = 0; while(l < v.size()){ int r = l + 1; while(r < v.size() && v[l].first == v[r].first) ++r; long long d = v[l].first * 1LL * v[l].first; for(int i = l; i < r; ++i){ int id = v[i].second; auto it = s.upper_bound(make_pair(id, -1)); assert(it->first == id); assert(it != s.begin()); auto R = *it; --it; auto L = *it; s.erase(L), s.erase(R); L.second = R.second; auto nd = get(0, 0, n, L.first, L.second); res = max(res, nd.ans - d); s.insert(L); } l = r; } cout << res << endl; return 0; }
