一.基本知识
1. 数学知识
(1)在二叉树的第i层上最多有2^(i-1)个节点
(2)深度为k的二叉树最多有2^(k)-1 个节点
(3)对任意二叉树,若叶子节点数为n0,度(节点拥有子树的个数)为2的节点数为n2,则 n0==n2+1
(4)对于具有n个节点的完全二叉树,如果按照对满二叉树节点连续编号的方式,对所有节点从1开始顺序编号,则对于任意序号为i的节点有:
如果 i==1 ,则没有双亲节点。i>1 ,则双亲节点(是同一个节点)的序号为“i/2”
如果 2i <= n,则节点i的左孩子节点序号为 2i ,否则就没有左孩子
如果 2i + 1 <= n,则节点i的右孩子节点序号为 2i+1 ,否则就没有右孩子
以上知识可以自己画图进行验证,也可以自己进行数学论证(反正我是不会的了~_~)
二. 二叉树的创建(二叉链表)
节点定义:
typedef struct Node {
char data ;
struct Node * Lchild ;
struct Node * Rchild ;
} BiNode ;
1.先序创建:
(1)第一种方法
BiNode *CreteBitree()
{
BiNode *p;
char ch ;
cin >> ch ;
if(ch == '#')
return NULL;
else {
p= (BiNode *)malloc(sizeof(BiNode));
p->data = ch ;
p->Lchild=CreteBitree();
p->Rchild=CreteBitree();
}
return p;
}
(2)第二种方法
void CreteBitree(BiNode **root)
{
char ch ;
cin >> ch ;
if( ch == '#' )
*root= NULL;
else {
*root = (BiNode *)malloc(sizeof(BiNode));
(*root)->data = ch;
CreteBitree(&(*root)->Lchild);
CreteBitree(&(*root)->Rchild);
}
}
三.二叉树的遍历
1.递归遍历
void PreOrder(BiNode *root)
{
if(root)
{
cout << root->data ;
PreOrder(root->Lchild);
PreOrder(root->Rchild);
}
}
void InOrder(BiNode *root)
{
if(root)
{
InOrder(root->Lchild);
cout << root->data ;
InOrder(root->Rchild);
}
}
void PostOrder(BiNode *root)
{
if(root)
{
PostOrder(root->Lchild);
PostOrder(root->Rchild);
cout << root->data ;
}
}
完整代码:
#include<iostream>
using namespace std;
typedef struct Node {
char data ;
struct Node * Lchild ;
struct Node * Rchild ;
} BiNode ;
void CreteBitree(BiNode **root)
{
char ch ;
cin >> ch ;
if( ch == '#' )
*root= NULL;
else {
*root = (BiNode *)malloc(sizeof(BiNode));
(*root)->data = ch;
CreteBitree(&(*root)->Lchild);
CreteBitree(&(*root)->Rchild);
}
}
void PreOrder(BiNode *root)
{
if(root)
{
cout << root->data ;
PreOrder(root->Lchild);
PreOrder(root->Rchild);
}
}
void InOrder(BiNode *root)
{
if(root)
{
InOrder(root->Lchild);
cout << root->data ;
InOrder(root->Rchild);
}
}
void PostOrder(BiNode *root)
{
if(root)
{
PostOrder(root->Lchild);
PostOrder(root->Rchild);
cout << root->data ;
}
}
int main(void)
{
BiNode *root;
cout << "Please input the string :" << endl ;
CreteBitree(&root);
cout<< "递归!!!先序遍历:" << endl ;
PreOrder(root);
cout << endl;
cout<< "中序遍历:" << endl ;
InOrder(root);
cout << endl;
cout<< "后序遍历:" << endl ;
PostOrder(root);
cout << endl ;
return 0;
}
所创建的树的形状:
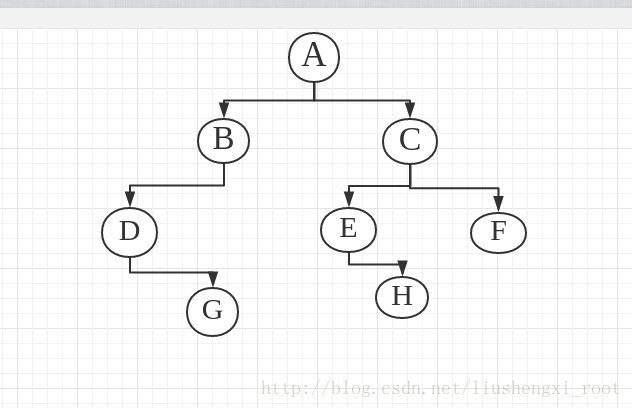
运行结果:
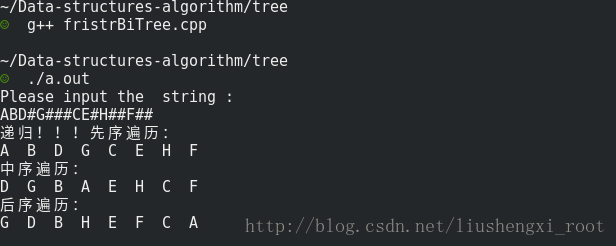
可以看到结果是正确的!!!
备注:以上的的代码均假设输入了正确的字符,没有进行错误处理。
下一篇将诉说二叉树的非递归遍历。

