Leetcode中级算法-动态规划02

题目：不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:

输入: m = 7, n = 3
输出: 28

原题链接：https://leetcode-cn.com/explore/interview/card/top-interview-questions-medium/51/dynamic-programming/105/

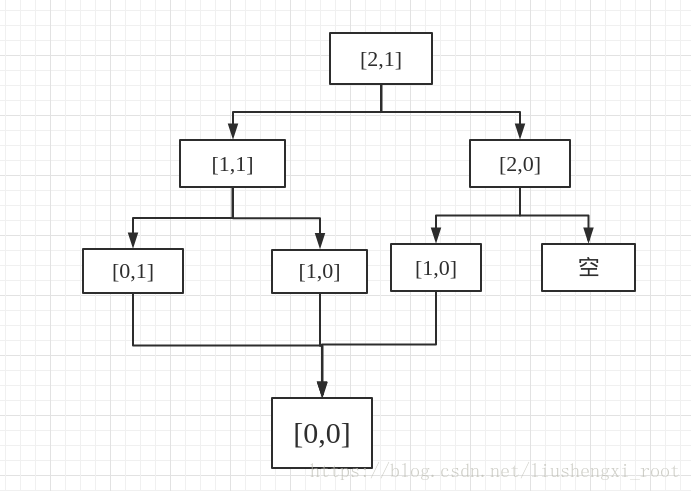
做题感性思路：首先我们还是按照DP的思路去思考问题。我们以3行2列的地图为例，发现想要到达[2，1]的前一个状态必然是[1，1]和[2，0] 其中之一，又想到求解的是总的路径，那毫无疑问就是将他们加起来。于是乎我们得到了我们的状态转移方程。

说明：在这幅图中，我们可以看到有的状态的前一个状态并不是有两种情况。有的可能只有右边，有的可能只有左边。

具体如何实现：用一个二维的path数组，其值用来表示到达该点的路径数量。那么就是求解核心就是 “path[i][j] = path[i - 1][j] + path[i][j - 1] ” ，考虑[1,10], [10,1]这样的特殊输入，进行path的初始化即可。

通过源代码：

#include<iostream>
#include<vector>
using namespace std;
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int> >  path(m, vector<int>(n, 0));

        path[0][0] = 1 ;
        if ( n > 1 )
            path[0][1] = 1 ;
        if ( m > 1 )
            path[1][0] = 1 ;

        for (int i =  0 ; i < m ; ++i)
        {
            for (int j = 0 ; j < n; ++j)
            {
                if ( i - 1 < 0  && j - 1 > 0 )
                    path[i][j] =  path[i][j - 1];

                if ( j - 1 < 0  && i - 1 > 0)
                    path[i][j] =  path[i - 1][j];

                if ((i - 1) >= 0 && (j - 1) >= 0 )
                    path[i][j] = path[i - 1][j] + path[i][j - 1];
            }
        }
        return path[m - 1][n - 1];
    }
};