主串 s:A B D A B C A B C
子串 t: A B C A B
问题:在主串 s 中是否存在一段 t 的子串呢?
形如上述问题,就是串匹配类问题。【串匹配——百度百科】
串匹配问题是一项有着非常多应用的重要技术,KMP匹配算法就是其中一种高效的字符串匹配算法。
在KMP算法之前先介绍一下BF算法,BF算法又名暴力匹配算法,该算法在匹配的时候把子串依次从主串的起始位置开始匹配,若匹配失败再从主串的下一个位置开始,子串重新从头开始匹配……
BF算法
int BF(char *str, char *sub)
{//暴力匹配算法
int i = 0; //遍历主串
int j = 0; //遍历子串
int k = i; //记录每次从主串匹配的起始位置
while (i < strlen(str) && j < strlen(sub))
{
if (str[i] == sub[j]) //当前下标位置匹配
{
++i;
++j;
}
else //当前下标位置不匹配
{
if(strlen(str) - i <= strlen(sub) ) return -1;//优化,如果主串剩余的长度没有子串长,则肯定不匹配
j = 0; //子串从头开始匹配
i = ++k; //匹配失败,i从主串的下一位置开始
}
}
if (j >= strlen(sub)) //子串遍历完,说明找到了对应的位置
{
return k;
}
else //子串没有遍历完,说明无该子串
return -1;
}
可以看到,BF算法是一种非常笨的算法,执行效率不高,那么有没有更优化的算法呢?
当然有啦,就是本文所讲的 KMP 算法。
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。
KMP算法的核心在于求Next子串,Next子串也叫模式串的前缀表,也就是模式串的最长公共前后缀
GetNext
next 前缀表中存放着当前字符之前的串的最大公共前后缀。这样做的好处就在于,当模式串与主串进行匹配时,如果出现失配情况可以根据保存在 next 中的信息迅速定位,无需从头开始匹配。
比如:下列匹配情况
X X X X X A B A X X X
A B A B C
A 与 C 不匹配,如果按照BF算法就要重头开始匹配了。但是我们发现,在模式串 A B A B C 中,有 A B 和 A B 相同的部分,那么是不是可以这样呢?
X X X X X A B A X X X
A B A B C
A B A B C
我们发现此时主串中的 A 与 模式串中的 A 匹配上了,先不管后续匹配情况如何,单就这个过程我们已经可以看出 KMP 算法的一些细节了。那么怎么让计算机实现我们上述的算法呢,这就不得不利用我们的next子串了。在本例中使用的以 -1,0 开头的next串格式,此格式便于在失配时(求next时失配或串匹配时失配) 快速回退。即 i = next(i) 这种形式。如下为求 next 的源码:
void GetNext(const char *sub, int *next)
{
int len = strlen(sub);
next[0] = -1; //此前缀表从-1开始,一些书籍上是从0开始
next[1] = 0;
int i = 0; //前缀
int j = 1; //后缀
while(j < len-1) //len-1 模式串中最后一个字符无需求前缀表
{
if (i == -1 || sub[i] == sub[j]) //匹配结束 || 匹配成功 ,写入next
{
next[++j] = ++i;
//++i;
//++j;
}
else //匹配失败,i回退
{
i = next[i];
}
}
}
KMP匹配过程演示
//从主串pos位置开始查找,默认从头开始
int KMP(const char* str, const char* sub, int pos = 0 )
{
int len_str = strlen(str);
int len_sub = strlen(sub);
if (pos < 0 || pos >= lenstr) return -1;//位置非法,查找失败
char* next = (char*)malloc(sizeof(char)*len_sub); //构建前缀表
GetNext(sub, next);
int i = pos; //主串 //从pos位置开始查找
int k = 0; //模式串/next
while(i < len_str && k < len_sub)
{
if(k == -1 || str[i] == sub[k]) //k==-1匹配结束(失败)|| 匹配成功,向后移动
{
++k;++i;
}
else //匹配失败,查询next表,移动模式串重新比较
{
k = next[k];
}
}
free(next);
if(k == len_sub) //模式串遍历完,找到位置
{
return i-k;
}
else //主串已结束,未找到子串
{
return -1;
}
}
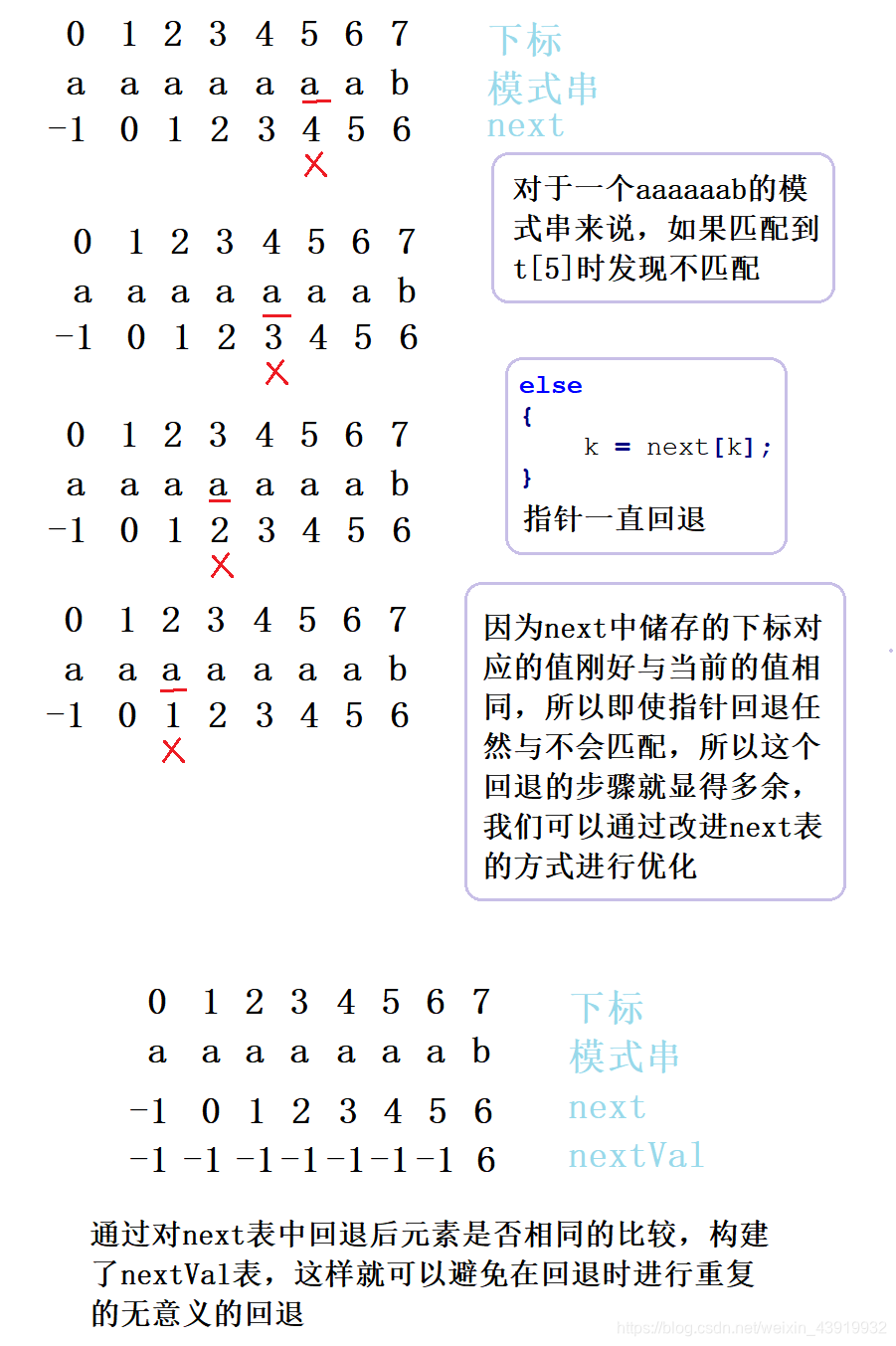
KMP算法的确是非常的智能,但是还有一种情况我们没有考虑到,比如一个 aaaaaaab 的模式串,在该模式串与主串匹配的时候,KMP算法也不是那么好用了。真是聪明难得糊涂一回,不过我们也有改进的方法,只需要去除next子串中多余重复的前缀并对其进行相应的优化即可,如下图所示:
优化:GetNextVal
void GetNextVal(const char* str, int* next)
{
int len = strlen(str);
next[0] = -1;
next[1] = 0;
int j = 1;
int k = 0;
while (j + 1 < len)
{
if (k == -1 || str[j] == str[k])
{
next[++j] = ++k;
}
else
{
k = next[k];
}
}
int* nextval = (int*)malloc(len * sizeof(int));
nextval[0] = -1;
for (int i = 1; i < len; i++)
{
if (str[i] == str[next[i]])
{
nextval[i] = nextval[next[i]];
}
else
{
nextval[i] = next[i];
}
}
for (int i = 0; i < len; i++)
{
next[i] = nextval[i];
}
free(nextval);
}