Farthest Nodes in a Tree
Given a tree (a connected graph with no cycles), you have to find the farthest nodes in the tree. The edges of the tree are weighted and undirected. That means you have to find two nodes in the tree whose distance is maximum amongst all nodes.
Input
starts with an integer T (≤ 10), denoting the number of test cases. Each case starts with an integer n (2 ≤ n ≤ 30000) denoting the total number of nodes in the tree. The nodes are numbered from 0 to n-1. Each of the next n-1 lines will contain three integers u v w (0 ≤ u, v < n, u ≠ v, 1 ≤ w ≤ 10000) denoting that node u and v are connected by an edge whose weight is w. You can assume that the input will form a valid tree.
Output
For each case, print the case number and the maximum distance.
Sample Input
2
4
0 1 20
1 2 30
2 3 50
5
0 2 20
2 1 10
0 3 29
0 4 50
Sample Output
Case 1: 100
Case 2: 80
这个题刚开始一直不理解(这道题是第一次接触树的直径),可后来看看了看学长给我板子。我去咋这么简单emmm。只要从任意一个节点出发然后找到距离他最远的节点,然后再让这个最远的出发去找距离这个最远的,这两个节点的距离就是树的直径!
这就是一个简单的板子题
#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
typedef pair<int,int> pa;
bool flag[100100];
int step[100100];
vector<pa>v[100100];
int a,b,c,sum;
int t,n;
int dfs(int x)
{
sum=0;
memset(flag,0,sizeof flag);
memset(step,0,sizeof step);
queue<int>q;
q.push(x);
flag[x]=1;
int yy=0;
while(!q.empty() )
{
int xx=q.front() ;
q.pop() ;
if(step[xx]>sum)
{
sum=step[xx];
yy=xx;
}
pa p;
for(int i=0;i<v[xx].size() ;i++)
{
p=v[xx][i];
int y=p.first ;
if(!flag[y])
{
flag[y]=1;
step[y]=step[xx]+p.second;
q.push(y);
}
}
}
return yy;
}
int main()
{
ios::sync_with_stdio(false);
cin>>t;
for(int i=1;i<=t;i++)
{
cin>>n;
for(int k=0;k<n;k++)
v[k].clear() ;
for(int j=1;j<n;j++)
{
cin>>a>>b>>c;
v[a].push_back(make_pair(b,c));//双向存储便于查找
v[b].push_back(make_pair(a,c));
}
dfs(dfs(0));
cout<<"Case "<<i<<": "<<sum<<endl;
}
return 0;
}
E-Computer
描述
一所学校不久前买了第一台电脑(所以这台电脑的ID是1)。近年来,学校购买了N-1新电脑。每台新电脑都连接到一台先前安装的电脑上。学校的管理人员担心网络运行缓慢,希望知道第i台计算机需要发送信号的最大距离si(即到最远计算机的电缆长度)。您需要提供此信息。
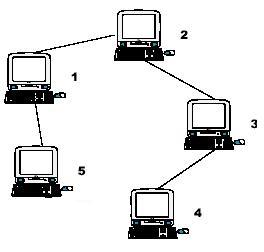
提示:示例输入与此图对应。从图中,你可以看到计算机4离1最远,所以s1=3。计算机4和5是距离2最远的,所以s2=2。计算机5是离3最远的,所以s3=3。我们也得到了s4=4,s5=4。
输入
输入文件包含多组测试样例。在每组样例中,第一行中都有自然数n(n<=10000),然后是(n-1)行,其中包含对计算机的描述。第i行包含两个自然数-第i计算机所连接的计算机和用于连接的电缆长度。电缆总长度不超过10^9。输入行中的数字用空格分隔。
输出
对于每组样例,输出n行。第i行第i台计算机的到其他计算机的最大长度Si(1<=i<=n)。
样例输入
5 1 1 2 1 3 1 1 1样例输出
3 2 3 4 4提示
示例输入与此图对应。从图中,你可以看到计算机4离1最远,所以s1=3。计算机4和5是距离2最远的,所以s2=2。计算机5是离3最远的,所以s3=3。我们也得到了s4=4,s5=4。
从一个点出发寻找到距离它最远的点,然后在从这个点出发寻找距离它最远的点中间记录每个节点的最远路程,这样算的的路径都是距离该节点的最远路径,然后再从距离这个点的最远的点在进行dfs还更新节点距离,那么最后的结果就是了
#include<iostream>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
typedef pair<int,int> pa;
int n,maxlen,s;
vector<pa>v[100100];
int dp[100100];
int dfs(int x,int y,int l)
{
if(maxlen<=l)
{
maxlen=l;
s=x;
}
pa p;
for(int i=0;i<v[x].size() ;i++)
{
p=v[x][i];
if(p.first ==y) continue;
else
{
dfs(p.first ,x,l+p.second);
dp[p.first]=max(dp[p.first],l+p.second);
}
}
}
int main()
{
while(cin>>n)
{
int x,y;
memset(dp,0,sizeof dp);
for(int i=0;i<=n;i++) v[i].clear() ;
for(int i=2;i<=n;i++)
{
cin>>x>>y;
v[x].push_back(make_pair(i,y));
v[i].push_back(make_pair(x,y));
}
s=0;
maxlen=0;
maxlen=0;
dfs(1,-1,0);
dfs(s,-1,0);
dfs(s,-1,0);
for(int i=1;i<=n;i++) cout<<dp[i]<<endl;
}
return 0;
}