P1196 [NOI2002]银河英雄传说(并查集)
本题关键
用两个一维数组表示了一个稀疏的二维数组。
这两个一维数组一个表示祖先(就是最前面那个),一个表示距离祖先的距离。
并且还有一个关键点是,距离祖先的距离是在并查集中动态更新的。
题目描述
公元五八○一年,地球居民迁至金牛座α第二行星,在那里发表银河联邦创立宣言,同年改元为宇宙历元年,并开始向银河系深处拓展。
宇宙历七九九年,银河系的两大军事集团在巴米利恩星域爆发战争。泰山压顶集团派宇宙舰队司令莱因哈特率领十万余艘战舰出征,气吞山河集团点名将杨威利组织麾下三万艘战舰迎敌。
杨威利擅长排兵布阵,巧妙运用各种战术屡次以少胜多,难免恣生骄气。在这次决战中,他将巴米利恩星域战场划分成30000列,每列依次编号为1, 2, …,30000。之后,他把自己的战舰也依次编号为1, 2, …, 30000,让第i号战舰处于第i列(i = 1, 2, …, 30000),形成“一字长蛇阵”,诱敌深入。这是初始阵形。当进犯之敌到达时,杨威利会多次发布合并指令,将大部分战舰集中在某几列上,实施密集攻击。合并指令为M i j,含义为第i号战舰所在的整个战舰队列,作为一个整体(头在前尾在后)接至第j号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增
大。 然而,老谋深算的莱因哈特早已在战略上取得了主动。在交战中,他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。
在杨威利发布指令调动舰队的同时,莱因哈特为了及时了解当前杨威利的战舰分布情况,也会发出一些询问指令:C i j。该指令意思是,询问电脑,杨威利的第i号战舰与第j号战舰当前是否在同一列中,如果在同一列中,那么它们之间布置有多少战舰。
作为一个资深的高级程序设计员,你被要求编写程序分析杨威利的指令,以及回答莱因哈特的询问。
最终的决战已经展开,银河的历史又翻过了一页……
输入输出格式
输入格式:
输入文件galaxy.in的第一行有一个整数T(1<=T<=500,000),表示总共有T条指令。
以下有T行,每行有一条指令。指令有两种格式:
-
M i j :i和j是两个整数(1<=i , j<=30000),表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令,并且保证第i号战舰与第j号战舰不在同一列。
- C i j :i和j是两个整数(1<=i , j<=30000),表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。
输出格式:
输出文件为galaxy.out。你的程序应当依次对输入的每一条指令进行分析和处理:
如果是杨威利发布的舰队调动指令,则表示舰队排列发生了变化,你的程序要注意到这一点,但是不要输出任何信息;
如果是莱因哈特发布的询问指令,你的程序要输出一行,仅包含一个整数,表示在同一列上,第i 号战舰与第j 号战舰之间布置的战舰数目。如果第i 号战舰与第j号战舰当前不在同一列上,则输出-1。
输入输出样例
说明
【样例说明】
战舰位置图:表格中阿拉伯数字表示战舰编号
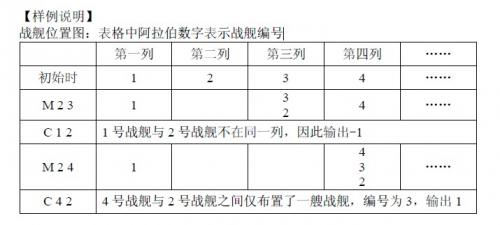
解答:
参考洛谷题解
解题报告
初见这道题,首先想到的方法当然是直接模拟,模拟每一次指令。当然这种方法对于小数据行得通,但对于此题的500,000个指令,肯定超时。
因此我们就要想其它方法。
先来分析一下这些指令的特点,很容易发现对于每个M指令,只可能一次移动整个队列,并且是把两个队列首尾相接合并成一个队列,不会出现把一个队列分开的情况,因此,我们必须要找到一个可以一次操作合并两个队列的方法。
再来看下C指令:判断飞船i和飞船j是否在同一列,若在,则输出它们中间隔了多少艘飞船。我们先只看判断是否在同一列,由于每列一开始都只有一艘飞船,之后开始合并,结合刚刚分析过的M指令,很容易就想到要用并查集来实现。
定义一个数组fa,fa[i]表示飞船i的祖先节点,即其所在列的队头。再定义一个用于查找飞船祖先的函数find,在每次递归找祖先的同时更新fa,压缩路径,大大减小以后的时间消耗。初始时对于每个fa[i]都赋值为i,合并时就先分别查找飞船i和飞船j的祖先,然后将飞船i的祖先的祖先(即fa[飞船i的祖先])赋值为飞船j的祖先。最后每次判断时只需要找到飞船i和飞船j的祖先,判断是否是同一艘飞船,若是,则在同一列,反之,则不在。
现在,判断是否在同一列以及如何一次操作合并两个队列的问题已经解决,但还有问题需要解决:如何在以上方法的基础上,进一步得到两艘飞船之间的飞船数量呢?
我们先来分析一下:两艘飞船之间的飞船数量,其实就是艘飞船之间的距离,那么,这就转换为了一个求距离的问题。两艘飞船都是在队列里的,最简单的求距离的方法就是前后一个一个查找,但这个方法太低效,会超时。看见多次求两个点的距离的问题,便想到用前缀和来实现:开一个front数组,front[i]表示飞船i到其所在队列队头的距离,然后飞船i和飞船j之间的飞船数量即为它们到队头的距离之差减一,就是abs(front[i]-front[j])-1。
解决了如何高效得到两艘飞船之间飞船数量的问题,便又发现了新的问题:如何在之前方法的基础上,得到每艘飞船和队头的距离呢?
来分析一下现在已经使用的算法——并查集,它的特点就是不是直接把一个队列里的所有飞船移到另一个队列后面,而是通过将要移动的队列的队头连接到另一个队列的队头上,从而间接连接两个队列。因此,我们在这个算法的基础上,每次只能更新一列中一艘飞船到队头的距离(如果更新多艘的话并查集就没有意义了)。
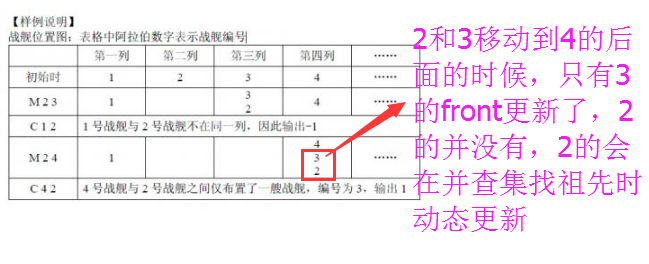
那么,该更新哪艘飞船呢?现在我们已经知道,使用并查集合并两个队列时只改变队头的祖先,而这个队列里其它飞船的祖先还是它原来的队头,并没有更新,所以这个队列里的其它飞船在队列合并之后,仍然可以找到它原来的队头,也就可以使用它原来队头的数据,因此,在每次合并的时候,只要更新合并前队头到目前队头的距离就可以了,之后其它的就可以利用它来算出自己到队头的距离。
理清了思路,但又有问题出现:该怎样更新呢?该怎么计算呢?
更新很容易,我们来分析一下:对于原来的队头,它到队头的距离为0,当将它所在的队列移到另一个队列后面时,它到队头的距离就是排在它前面的飞船数,也就是合并前另一个队列的飞船数量。因此,就知道该怎样实现了,我们再建一个数组num,num[i]表示以i为队头的队列的飞船数量,初始时都是1,在每次合并的时候,fx为合并前飞船i的队头,fy为合并前飞船j的队头,每次合并时,先更新front[fx],即给它加上num[fy],然后开始合并,即fa[fx]=fy,最后更新num, num[fy]+= num[fx];num[fx]=0。
现在就差最后一步了:如何计算每个飞船到队头的距离。再来分析一下:对于任意一个飞船,我们都知道它的祖先(不一定是队头,但一定间接或直接指向队头),还知道距离它祖先的距离。对于每一个飞船,它到队头的距离,就等于它到它祖先的距离加上它祖先到队头的距离,而它的祖先到队头的距离,也可以变成类似的。可以递归实现,由于每一次更新都要用到已经更新完成的祖先到队头的距离,所以要先递归找到队头,然后在回溯的时候更新(front[i]+=front[fa[i]]),可以把这个过程和查找队头的函数放在一起。
源代码
1 #include<bits/stdc++.h> 2 using namespace std; 3 int fa[30001],front[30001],num[30001],x,y,i,j,n,T,ans; //fa[i]表示飞船i的祖先 4 //front[i]表示飞船i与其所在列队头的距离 5 //num[i]表示第i列的飞船数量 6 char ins; 7 int find(int n){ //查找祖先的函数 8 if(fa[n]==n)return fa[n]; 9 int fn=find(fa[n]); //先递归找到祖先 10 front[n]+=front[fa[n]]; //在回溯的时候更新front(因为更新时要用到正确的front[祖先], 11 //所以只能在回溯的时候更新) 12 return fa[n]=fn; 13 } 14 int main(){ 15 cin>>T; 16 for(i=1;i<=30000;++i){ //定初值 17 fa[i]=i; 18 front[i]=0; 19 num[i]=1; 20 } 21 while(T--){ 22 cin>>ins>>x>>y; 23 int fx=find(x); //fx为x所在列的队头 24 int fy=find(y); //fy同上 25 if(ins=='M'){ 26 front[fx]+=num[fy]; //更新front[x所在列队头(现在在y所在队列后面)] 27 //即加上y所在队列的长度 28 fa[fx]=fy; //将fy设为fx的祖先 29 num[fy]+=num[fx]; //更新以fy为队头队列的长度 30 num[fx]=0; //以fx为队头的队列已不存在,更新 31 } 32 if(ins=='C'){ 33 if(fx!=fy)cout<<"-1"<<endl; //若x和y的祖先不相同,则不在同一列 34 else cout<<abs(front[x]-front[y])-1<<endl; //否则利用x和y离队头的距离算 35 //出它们的距离 36 } 37 } 38 return 0; 39 }
测评结果
Accepted