算法与数据结构---8.2、过河卒-搜索解法取正
一、总结
一句话总结:
过河卒搜索解法取正就是将过河卒递推表达式中负数的情况转化成正数的情况,可以通过给图上的每个点加上一个数来实现,这样就少了很多负数的判断,并且对结果也没有影响
1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 int hx[9]={0,-2,-1,1,2,2,1,-1,-2}; 5 int hy[9]={0,1,2,2,1,-1,-2,-2,-1}; 6 long long f[25][25]; 7 long long find(int x,int y){ 8 //如果缓存里面有,就从缓存里面拿 9 //否则计算结果存入缓存 10 if(f[x][y]!=-1) return f[x][y]; 11 else{ 12 //f[i][j]=f[i-1][j]+f[i][j-1] 13 return f[x][y]=find(x-1,y)+find(x,y-1); 14 } 15 } 16 17 int main(){ 18 int bx,by,mx,my; 19 cin>>bx>>by>>mx>>my; 20 bx+=2;by+=2;mx+=2;my+=2; 21 memset(f,-1,sizeof(f)); 22 f[2][2]=1; 23 for(int i=1;i<=bx;i++) f[i][1]=0; 24 for(int i=1;i<=by;i++) f[1][i]=0; 25 //将马控制的点加入到f数组 26 for(int i=0;i<=8;i++){ 27 f[mx+hx[i]][my+hy[i]]=0; 28 } 29 30 cout<<find(bx,by)<<endl; 31 return 0; 32 }
二、过河卒
1、题目描述
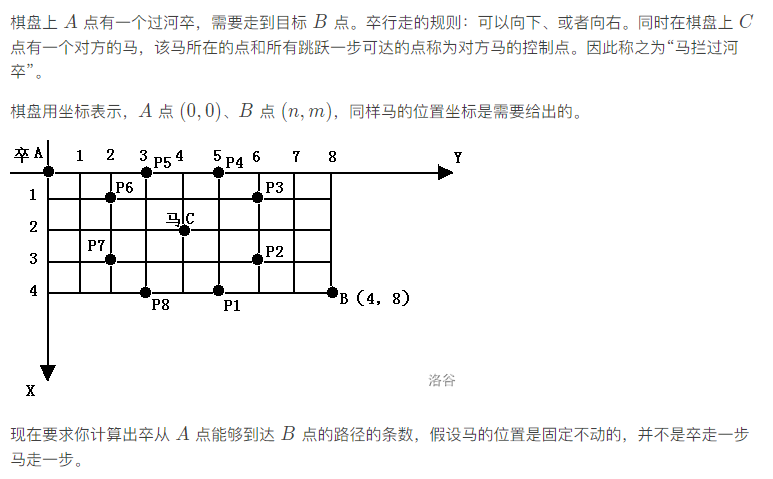

/*
题目位置:
P1002 过河卒 - 洛谷
https://www.luogu.com.cn/problem/P1002
*/
/*
样例输入:6 6 3 3
样例输出:6
b点是(6,6),马的坐标是(3,3)
A是A点 , B是B点, M是马的位置, X是被马拦着不能走的点
A 0 0 0 0 0 0
0 0 X 0 X 0 0
0 X 0 0 0 X 0
0 0 0 M 0 0 0
0 X 0 0 0 X 0
0 0 X 0 X 0 0
0 0 0 0 0 0 B
其中每个点的值代表的是当前这个点会有几条路径用过这个点
(路径指的是从A到B的路径)
1 1 1 1 1 1 1
1 2 X 1 X 1 2
1 X 0 1 1 X 2
1 1 1 M 1 1 3
1 X 1 1 0 X 3
1 1 X 1 X 0 3
1 2 2 3 3 3 6
*/
2、搜索解法
博客对应课程的视频位置:8.1、过河卒-搜索解法
https://www.fanrenyi.com/video/27/288
1 /*
2
3 递推表达式:
4 卒子可以向下走和向右走
5 如果设f[i][j]表示走到(i,j)点的路径总数
6 对应的走到f[i][j]只能从上边来或者从左边来
7 f[i][j]=f[i-1][j]+f[i][j-1]
8
9
10 简单的思考:
11 如果没有这个马,搜索应该怎么做
12
13 递归:
14 递归的终止条件:起点
15 递归的递推表达式:f[i][j]=f[i-1][j]+f[i][j-1]
16 递归的返回值:路径条数
17
18 初始值:f[0][0]=1
19
20 如果有马的情况
21 递归的终止条件:起点或者马控制的区域
22
23
24 注意:
25 1、本题的路径条数是超过int的,所以要用long long
26 2、使用递推表达式f[i][j]=f[i-1][j]+f[i][j-1]时,
27 因为有i-1、j-1,所以要考虑i、j是否大于1的情况
28 3、初始化的时候,不能直接初始化i=0和j=0对应的两条线,
29 因为当马的控制点在这两条线上时,控制点后的点是达不到的
30
31
32 思考:
33 1 1 1 1 1 1 1
34 1 2 X 1 X 1 2
35 1 X 0 1 1 X 2
36 1 1 1 M 1 1 3
37 1 X 1 1 0 X 3
38 1 1 X 1 X 0 3
39 1 2 2 3 3 3 6
40 这里初始化的时候能直接初始化i=0和j=0对应的两条线么
41 不能,因为如果这样初始化后,当马的位置如果是(4,0),
42 那么(5,0)的位置本来是去不了的,
43 但是这样初始化却会初始化为1
44
45
46 */
47 #include <iostream>
48 #include <cstring>
49 using namespace std;
50 int hx[9]={0,-2,-1,1,2,2,1,-1,-2};
51 int hy[9]={0,1,2,2,1,-1,-2,-2,-1};
52 long long f[25][25];
53 long long find(int x,int y){
54 //如果缓存里面有,就从缓存里面拿
55 //否则计算结果存入缓存
56 if(f[x][y]!=-1) return f[x][y];
57 else{
58 //f[i][j]=f[i-1][j]+f[i][j-1]
59 if(x-1>=0&&y-1>=0) return f[x][y]=find(x-1,y)+find(x,y-1);
60 else if(x-1>=0) return f[x][y]=find(x-1,y);
61 else if(y-1>=0) return f[x][y]=find(x,y-1);
62 else return f[x][y]=0;
63 }
64 }
65
66 int main(){
67 int bx,by,mx,my;
68 cin>>bx>>by>>mx>>my;
69 memset(f,-1,sizeof(f));
70 f[0][0]=1;
71
72 //将马控制的点加入到f数组
73 for(int i=0;i<=8;i++){
74 int now_x=mx+hx[i];
75 int now_y=my+hy[i];
76 if(now_x>=0&&now_y>=0){
77 f[now_x][now_y]=0;
78 }
79 }
80
81 cout<<find(bx,by)<<endl;
82 return 0;
83 }
3、搜索解法取正
博客对应课程的视频位置:8.2、过河卒-搜索解法取正
https://www.fanrenyi.com/video/27/289
1 /* 2 3 递推表达式f[i][j]=f[i-1][j]+f[i][j-1] 4 需要 i-1 和 j-1, 5 6 int hx[9]={0,-2,-1,1,2,2,1,-1,-2}; 7 int hy[9]={0,1,2,2,1,-1,-2,-2,-1}; 8 9 而初始化马控制的点的时候会有 i-2, j-2 , 10 11 所以我们可以 把整个图向右下移动2, 12 右下移2也就是把每个点的横纵坐标都加2 13 这样i-1、j-1、i-2、j-2都不会为负数了 14 这样就省了很多if判断, 15 而且这样对问题不会有任何影响 16 17 18 A是A点 , B是B点, M是马的位置, X是被马拦着不能走的点 19 A 0 0 0 0 0 0 20 0 0 X 0 X 0 0 21 0 X 0 0 0 X 0 22 0 0 0 M 0 0 0 23 0 X 0 0 0 X 0 24 0 0 X 0 X 0 0 25 0 0 0 0 0 0 B 26 27 取正后,也就是每个点都右下移2后 28 0 0 0 0 0 0 0 0 0 29 0 0 0 0 0 0 0 0 0 30 0 0 A 0 0 0 0 0 0 31 0 0 0 0 X 0 X 0 0 32 0 0 0 X 0 0 0 X 0 33 0 0 0 0 0 M 0 0 0 34 0 0 0 X 0 0 0 X 0 35 0 0 0 0 X 0 X 0 0 36 0 0 0 0 0 0 0 0 B 37 38 39 */ 40 41 #include <iostream> 42 #include <cstring> 43 using namespace std; 44 int hx[9]={0,-2,-1,1,2,2,1,-1,-2}; 45 int hy[9]={0,1,2,2,1,-1,-2,-2,-1}; 46 long long f[25][25]; 47 long long find(int x,int y){ 48 //如果缓存里面有,就从缓存里面拿 49 //否则计算结果存入缓存 50 if(f[x][y]!=-1) return f[x][y]; 51 else{ 52 //f[i][j]=f[i-1][j]+f[i][j-1] 53 return f[x][y]=find(x-1,y)+find(x,y-1); 54 } 55 } 56 57 int main(){ 58 int bx,by,mx,my; 59 cin>>bx>>by>>mx>>my; 60 bx+=2;by+=2;mx+=2;my+=2; 61 memset(f,-1,sizeof(f)); 62 f[2][2]=1; 63 for(int i=1;i<=bx;i++) f[i][1]=0; 64 for(int i=1;i<=by;i++) f[1][i]=0; 65 //将马控制的点加入到f数组 66 for(int i=0;i<=8;i++){ 67 f[mx+hx[i]][my+hy[i]]=0; 68 } 69 70 cout<<find(bx,by)<<endl; 71 return 0; 72 }