本文会从递归反转整个单链表开始拓展
递归反转整个链表
先直接看实现代码:
ListNode reverse(ListNode head) {
if (head.next == null) return head;
ListNode last = reverse(head.next);
head.next.next = head;
head.next = null;
return last;
}
对于递归算法,最重要的就是明确递归函数的定义。具体来说,我们的 reverse 函数定义是这样的:
输入一个节点 head,将「以 head 为起点」的链表反转,并返回反转之后的头结点。
不过其中有两个地方需要注意:
1、递归函数要有 base case,也就是这句:
if (head.next == null) return head;
意思是如果链表只有一个节点的时候反转也是它自己,直接返回即可。
2、当链表递归反转之后,新的头结点是 last,而之前的 head 变成了最后一个节点,别忘了链表的末尾要指向 null:
head.next = null;
反转链表前 N 个节点
实现一个这样的函数:
// 将链表的前 n 个节点反转(n <= 链表长度)
ListNode reverseN(ListNode head, int n)
比如说对于下图链表,执行 reverseN(head, 3):
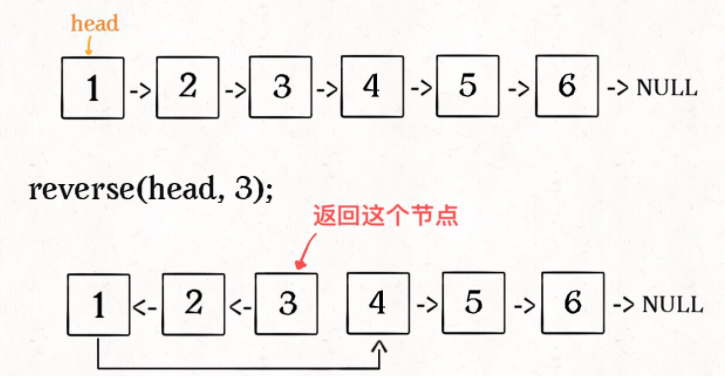
解决思路和反转整个链表差不多,只要稍加修改即可:
ListNode successor = null; // 后驱节点
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode last = reverseN(head.next, n - 1);
head.next.next = head;
// 让反转之后的 head 节点和后面的节点连起来
head.next = successor;
return last;
}
具体的区别:
1、base case 变为 n == 1,反转一个元素,就是它本身,同时要记录后驱节点。
2、刚才我们直接把 head.next 设置为 null,因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了,所以要记录后驱 successor(第 n + 1 个节点),反转之后将 head 连接上。
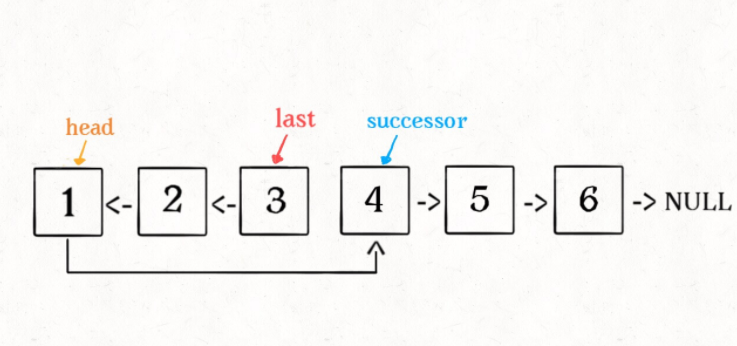
反转链表的一部分
给一个索引区间 [m,n](索引从 1 开始),仅仅反转区间中的链表元素。
ListNode reverseBetween(ListNode head, int m, int n)
首先,如果 m == 1,就相当于反转链表开头的 n 个元素嘛,也就是我们刚才实现的功能:
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
// 相当于反转前 n 个元素
return reverseN(head, n);
}
// ...
}
如果 m != 1 怎么办?如果我们把 head 的索引视为 1,那么我们是想从第 m 个元素开始反转对吧;如果把 head.next 的索引视为 1 呢?那么相对于 head.next,反转的区间应该是从第 m - 1 个元素开始的;那么对于 head.next.next 呢……
区别于迭代思想,这就是递归思想,所以我们可以完成代码:
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
return reverseN(head, n);
}
// 前进到反转的起点触发 base case
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}
值得一提的是,递归操作链表并不高效。和迭代解法相比,虽然时间复杂度都是 O(N),但是迭代解法的空间复杂度是 O(1),而递归解法需要堆栈,空间复杂度是 O(N)。
K个一组翻转链表

对这个链表调用 reverseKGroup(head, 2),即以 2 个节点为一组反转链表:
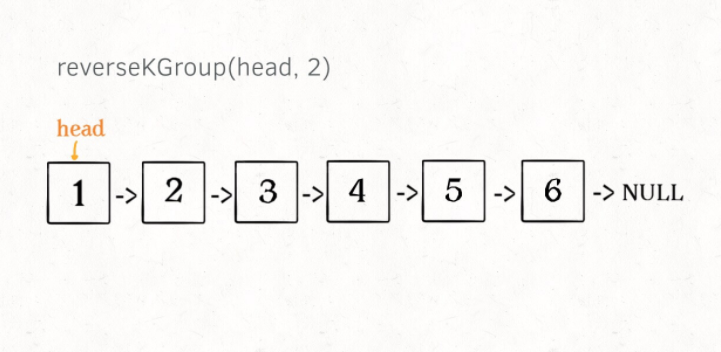
如果我设法把前 2 个节点反转,那么后面的那些节点怎么处理?后面的这些节点也是一条链表,而且规模(长度)比原来这条链表小,这就叫子问题。
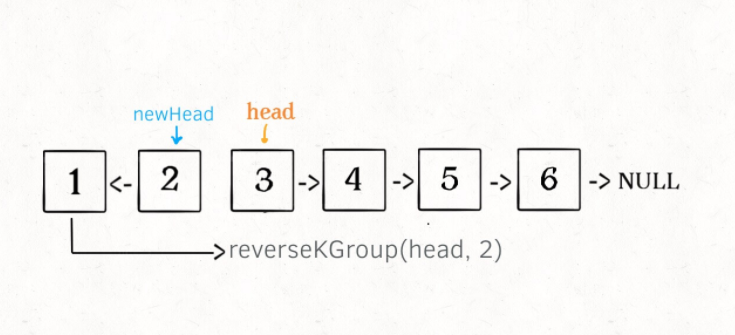
我们可以直接递归调用 reverseKGroup(cur, 2),因为子问题和原问题的结构完全相同,这就是所谓的递归性质。
发现了递归性质,就可以得到大致的算法流程:
1、先反转以 head 开头的 k 个元素。
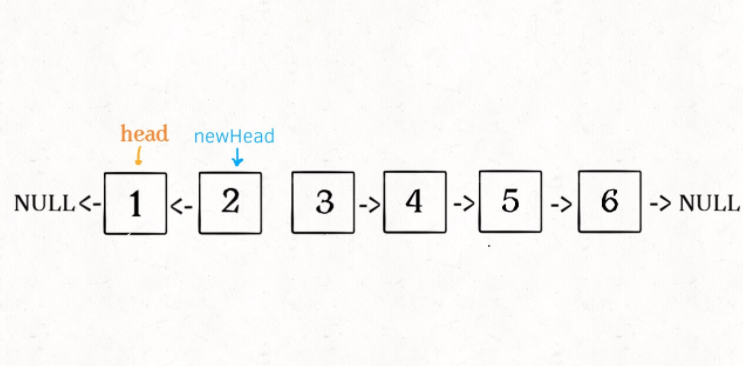
2、将第 k + 1 个元素作为 head 递归调用 reverseKGroup 函数。
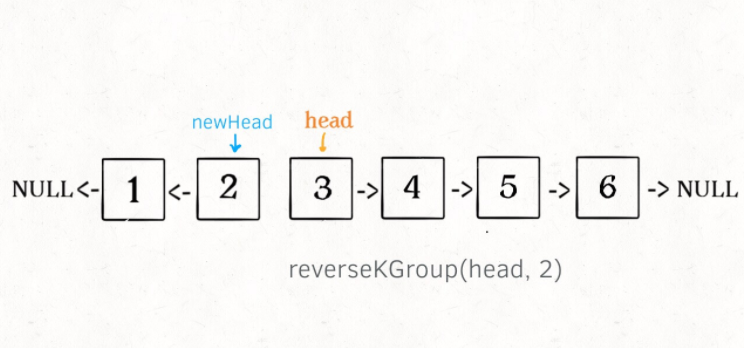
3、将上述两个过程的结果连接起来。
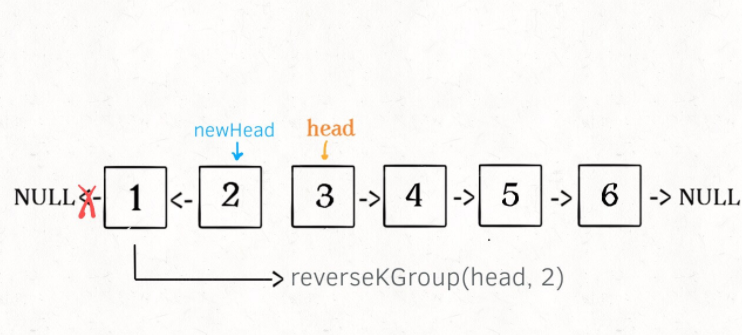
如果最后的元素不足 k 个,就保持不变。这就是 base case
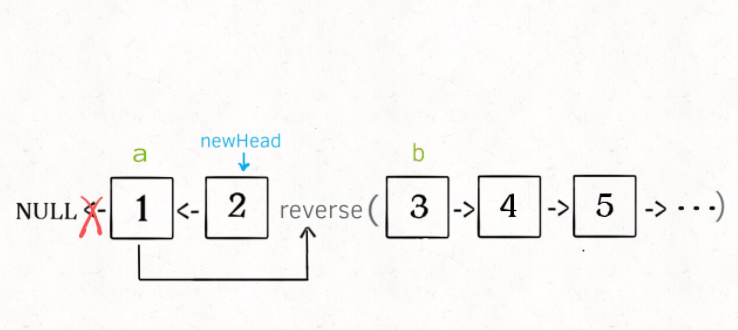
首先,我们要实现一个 reverse 函数反转一个区间之内的元素
/** 反转区间 [a, b) 的元素,注意是左闭右开 */
ListNode reverse(ListNode a, ListNode b) {
ListNode pre, cur, nxt;
pre = null; cur = a; nxt = a;
// while 终止的条件改一下就行了
while (cur != b) {
nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
// 返回反转后的头结点
return pre;
}
现在我们迭代实现了反转部分链表的功能,接下来就按照之前的逻辑编写 reverseKGroup 函数即可:
ListNode reverseKGroup(ListNode head, int k) {
if (head == null) return null;
// 区间 [a, b) 包含 k 个待反转元素
ListNode a, b;
a = b = head;
for (int i = 0; i < k; i++) {
// 不足 k 个,不需要反转,base case
if (b == null) return head;
b = b.next;
}
// 反转前 k 个元素
ListNode newHead = reverse(a, b);
// 递归反转后续链表并连接起来
a.next = reverseKGroup(b, k);
return newHead;
}
整个函数递归完成之后就是这个结果:
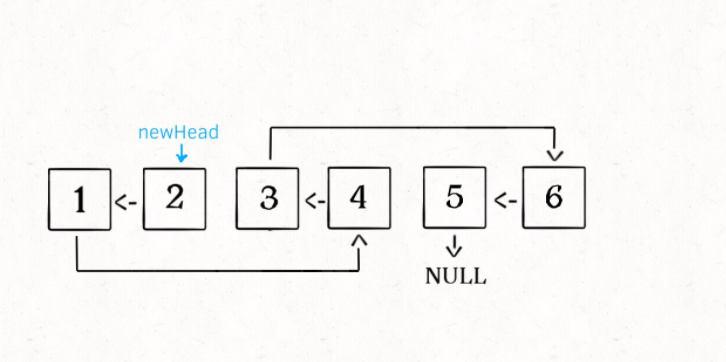
判断回文链表
寻找回文串的核心思想是从中心向两端扩展:
string palindrome(string& s, int l, int r) {
// 防止索引越界
while (l >= 0 && r < s.size()
&& s[l] == s[r]) {
// 向两边展开
l--; r++;
}
// 返回以 s[l] 和 s[r] 为中心的最长回文串
return s.substr(l + 1, r - l - 1);
}
判断一个字符串是不是回文串就简单很多,不需要考虑奇偶情况,只需要「双指针技巧」,从两端向中间逼近即可:
bool isPalindrome(string s) {
int left = 0, right = s.length - 1;
while (left < right) {
if (s[left] != s[right])
return false;
left++; right--;
}
return true;
}
判断回文单链表
借助二叉树后序遍历的思路,不需要显式反转原始链表也可以倒序遍历链表
void traverse(TreeNode root) {
// 前序遍历代码
traverse(root.left);
// 中序遍历代码
traverse(root.right);
// 后序遍历代码
}
链表其实也可以有前序遍历和后序遍历:
void traverse(ListNode head) {
// 前序遍历代码
traverse(head.next);
// 后序遍历代码
}
如果我想正序打印链表中的val值,可以在前序遍历位置写代码;反之,如果想倒序遍历链表,就可以在后序遍历位置操作:
/* 倒序打印单链表中的元素值 */
void traverse(ListNode head) {
if (head == null) return;
traverse(head.next);
// 后序遍历代码
print(head.val);
}
其实可以稍作修改,模仿双指针实现回文判断的功能:
// 左侧指针
ListNode left;
boolean isPalindrome(ListNode head) {
left = head;
return traverse(head);
}
boolean traverse(ListNode right) {
if (right == null) return true;
boolean res = traverse(right.next);
// 后序遍历代码
res = res && (right.val == left.val);
left = left.next;
return res;
}
这么做的核心逻辑实际上就是把链表节点放入一个栈,然后再拿出来,这时候元素顺序就是反的,只不过我们利用的是递归函数的堆栈而已。
优化空间复杂度
1、先通过「双指针技巧」中的快慢指针来找到链表的中点:
ListNode slow, fast;
slow = fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// slow 指针现在指向链表中点
2、如果 fast指针没有指向 null,说明链表长度为奇数,slow还要再前进一步:
if (fast != null)
slow = slow.next;
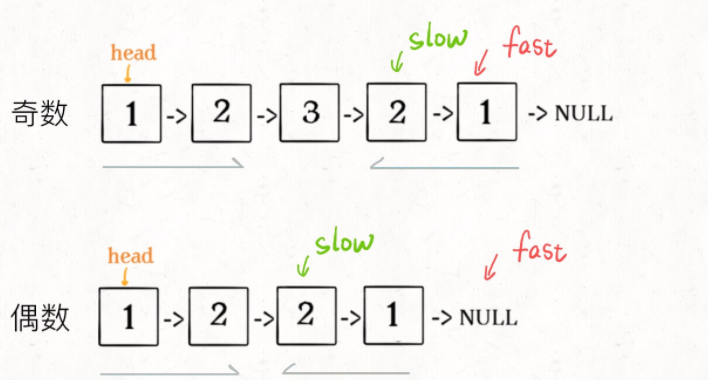
3、从slow开始反转后面的链表,现在就可以开始比较回文串了:
ListNode left = head;
ListNode right = reverse(slow);
while (right != null) {
if (left.val != right.val)
return false;
left = left.next;
right = right.next;
}
return true;
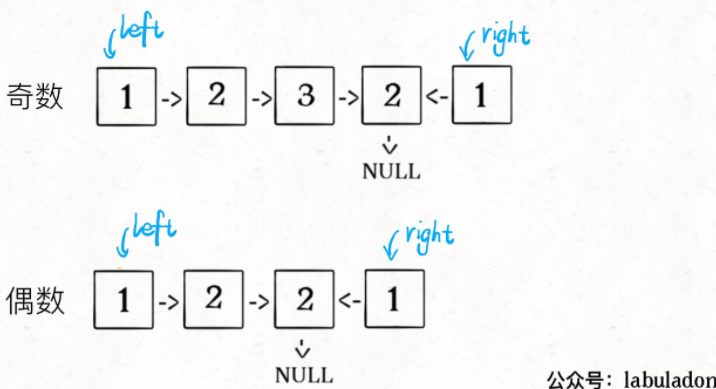
把上面 3 段代码合在一起就高效地解决这个问题了,其中reverse函数很容易实现:
ListNode reverse(ListNode head) {
ListNode pre = null, cur = head;
while (cur != null) {
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
return pre;
}
整体代码如下:
// 这个方法通过将链表中间后边的链表反转,因为后边的链表往前遍历不好遍历,所以反转之后往后遍历就相当于原来的链表往前遍历,这样就可以方便的和前边的链表作比较了
public boolean isPalindrome(ListNode head) {
ListNode slow = findMidNxt(head);
ListNode left = head;
// 将中间后边的链表反转之后,这样就可以方便的遍历反转后的链表来判断和左边的链表是否相同了
ListNode right = reverse(slow);
while(right!=null) {
if(right.val!=left.val) {
return false;
}
right = right.next;
left = left.next;
}
// left = head;
return true;
}
// 反转链表
public ListNode reverse(ListNode head) {
ListNode pre,cur,nxt;
pre = null;cur = head;nxt =head;
while(cur!=null) {
nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
return pre;
}
// 通过快慢指针找到中间的那个节点的后边那个节点
public ListNode findMidNxt(ListNode head) {
ListNode slow,fast;
slow = head;fast = head;
while(fast!=null&&fast.next!=null) {
slow = slow.next;
fast = fast.next.next;
}
// 如果fast指针没有指向null,说明链表长度为奇数,slow还要再前进一步
if(fast !=null) {
slow = slow.next;
}
return slow;
}
这种解法虽然高效,但破坏了输入链表的原始结构,能不能避免这个瑕疵呢?
其实这个问题很好解决,关键在于得到p, q这两个指针位置:
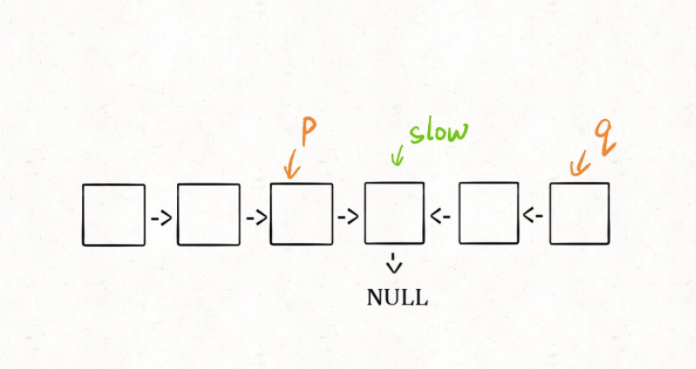
只要在函数 return 之前加一段代码即可恢复原先链表顺序:
p.next = reverse(q);
总结:
寻找回文串是从中间向两端扩展,判断回文串是从两端向中间收缩。对于单链表,无法直接倒序遍历,可以造一条新的反转链表,可以利用链表的后序遍历,也可以用栈结构倒序处理单链表。
具体到回文链表的判断问题,由于回文的特殊性,可以不完全反转链表,而是仅仅反转部分链表,将空间复杂度降到 O(1)。