1. 为什么需要素性测试?
我们其实已经知道有一些判断素数的方法,比如:
遍历测试:待测试数n与2,3,...√n做除法判断余数是否为零,如果没有任何一个数可以整除n,则说明n为素数
Wilson定理:对于给定的正整数n,n是素数的充要条件为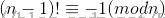
上面的方法都可以确定的判断出一个数是否为素数,但问题在于对于大整数,这两个算法都需要很大计算量和时间,能不能有一个更快速的判定算法呢?
答案是当前还没有一个更高效且能准确判定素数的方法。但借助随机算法和数论知识,已有可以非常高效且判定错误率很低的素数测试算法,即Millan_Rabin素性测试
2. 需要知道的知识
2.1 Fermat定理

费马定理的前提是a和n互质。当n本身就是素数的时候如果a<n那么a和n始终互素,费马定理是成立的,但n当不是素数,且a和n不互素的话不能用费马定理(也就是说费马定理不一定成立)
需要知道的是满足费马定理是素数的必要条件,但不是充分条件,也就是说是素数一定满足费马定理(如果一个数不满足费马定理就不是素数),但是满足费马定理的数字不一定是素数(称为伪素数,伪素数的数量较少,所以可以通过费马定理以比较大的概率判定一个数是否为素数)
令a=2,不满足2^(n-1) mod n = 1的n一定不是素数;如果满足的话则多半是素数。这样,一个比试除法效率更高的素性判断方法出现了:制作一张伪素数表,记录某个范围内的所有伪素数,那么所有满足2^(n-1) mod n = 1且不在伪素数表中的n就是素数。之所以这种方法更快,是因为我们可以使用二分法快速计算2^(n-1) mod n 的值,这在计算机的帮助下变得非常容易;在计算机中也可以用二分查找有序数列、Hash表开散列、构建Trie树等方法使得查找伪素数表效率更高。
那么伪素数的个数到底有多少?换句话说,如果我只计算2^(n-1) mod n的值,事先不准备伪素数表,那么素性判断出错的概率有多少?统计表明,在前10亿个自然数中共有50847534个素数,而满足2^(n-1) mod n = 1的合数n有5597个。这样算下来,算法出错的可能性约为0.00011。这个概率还是太高了,如果想免去建立伪素数表的工作,我们需要还需要改进素性判断的算法。
最简单的想法就是,我们刚才只考虑了a=2的情况。对于式子a^(n-1) mod n,取不同的a可能导致不同的结果。一个合数可能在a=2时通过了测试,但a=3时的计算结果却排除了素数的可能。于是,人们扩展了伪素数的定义,称满足a^(n-1) mod n = 1的合数n叫做以a为底的伪素数(pseudoprime to base a)。前10亿个自然数中同时以2和3为底的伪素数只有1272个,这个数目不到刚才的1/4。这告诉我们如果同时验证a=2和a=3两种情况,算法出错的概率降到了0.000025。容易想到,选择用来测试的a越多,算法越准确。通常我们的做法是,随机选择若干个小于待测数的正整数作为底数a进行若干次测试,只要有一次没有通过测试就立即把这个数扔回合数的世界。这就是Fermat素性测试。
人们自然会想,如果考虑了所有小于n的底数a,出错的概率是否就可以降到0呢?没想到的是,居然就有这样的合数,它可以通过所有a的测试(在满足费马定理前提的条件下)。Carmichael第一个发现这样极端的伪素数,他把它们称作Carmichael数。你一定会以为这样的数一定很大。错。第一个Carmichael数小得惊人,仅仅是一个三位数,561。前10亿个自然数中Carmichael数也有600个之多。Carmichael数的存在说明,我们还需要继续加强素性判断的算法。
2.2 二次探测定理

这个定理应该怎么理解呢?其实就是说,(x+1)(x-1)可以整除p,又因为p是素数,不可分割,所以要么是(x-1)这一部分整除了p(因为0<x<p,故x-1<p,所以x-1只能为0才能满足,所以此时x = 1),要么就是(x+1)整除了p(因为0<x<p,则1<x+1<p+1,故只有当x+1=p才能满足,此时x = p-1),所以满足条件的x=1或x=p-1
二次探测定理可以用来对费马定理做一个增强,以更高的概率确定一个数是否为素数,将两者融合,就可以得到Miller_Rabin算法。
3. Miller_Rabin定理

为什么说测试次数为k次,错误概率可降低之(1/4)^k呢?(这还是保守估计)
我的理解是,因为上面我们知道,同时通过2和3的费马测试的伪素数个数不到通过2的费马测试的个数的1/4,这还只是通过了费马测试,这里我们还进行了二次检测,所以错误率应该更低,且数字越大,能够同时通过更多数字费马测试的数越少(推测),所以错误率至少是(1/4)^k,实际中应该比这个还要低很多。
下面举个例子来说明Miller_Rabin算法判断素数的流程,我们来测试341是否为素数。首先可以验证341可以通过以2为底的Fermat测试,因为2^340 mod 341=1。如果341真是素数的话,那么2^170 mod 341只可能是1或340;当算得2^170 mod 341确实等于1时,我们可以继续查看2^85除以341的结果。我们发现,2^85 mod 341=32,这一结果并不满足x = 1或x = 340这一条件,所以和二次探测定理矛盾,这一结果摘掉了341头上的素数皇冠。
Miller-Rabin素性测试同样是不确定算法,我们把可以通过以a为底的Miller-Rabin测试的合数称作以a为底的强伪素数(strong pseudoprime)。第一个以2为底的强伪素数为2047。第一个以2和3为底的强伪素数则大到1 373 653。所以说Miller_Rabin算法可以看作Fermat测试的一个加强版,可以以更大的概率确定一个数是否为素数。再借助快速幂算法,同时可以加速这个进程,判定速度更快。
4. Miller_Rabin算法C++实现
#include <iostream> #include <stdlib.h> typedef long long int ll; using namespace std; ll quick_mul (ll a, ll b, ll mod) { ll res = 0; while(b) { if(b & 1) { res = (res + a) % mod; } a = (a + a) % mod; b >>= 1; } return res; } ll quick_pow(ll a, ll n, ll mod) { ll res = 1; while(n) { if(n & 1) { res = quick_mul(res, a, mod); } a = quick_mul(a, a, mod); n >>= 1; } return res; } bool Miller_Rabin(ll n) { if(n == 2) { return true; } if(n < 2 || !(n & 1)) { return false; } ll m = n-1, k = 0; while(!(m&1)) { k++; m >>= 1; } // printf("m = %lld, k = %lld ", m, k); int iter = 10; for(int i = 0; i < iter; i++) { ll a = rand() % (n-1) + 1; // printf("a = %lld ", a); ll x = quick_pow(a, m, n); // printf("x = %lld ", x); ll y; for(int j = 0; j < k; j++) { y = quick_pow(x, x, n); // printf("y = %lld ", y); if(y == 1 && x != 1 && x != n-1) { return false; } x = y; } if(y != 1) { return false; } } return true; } int main(void) { ll num; printf("Please input the num you want to test: "); scanf("%lld", &num); printf("%s ", Miller_Rabin(num) ? "yes" : "no"); }
参考
https://blog.csdn.net/ECNU_LZJ/article/details/72675595
http://www.matrix67.com/blog/archives/234
本文很大程度参考了这两篇博文,都写的很好,值得学习:)