远心镜头通常分为物方远心镜头、像方远心镜头和双侧远心镜头,在机器视觉领域,像方远心镜头不起作用。
双侧远心光路相对物方远心,在一定范围内,前后移动芯片位置,成像不变,这是它的一优势,但高昂也价格是它的不足。
另一方面物方远心可通过调节法兰距,同时使用过程中法兰距不发生大的变动,这时也能保证像质的良好,因此物方远心镜头基本上可满足大多数视觉系统中检
测的需求。
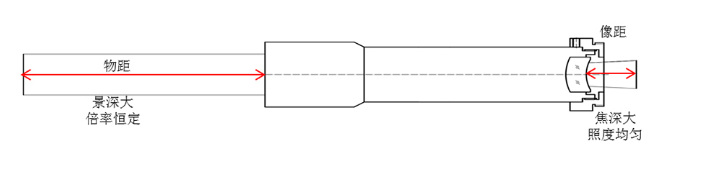
二、远心度
远心度描述了主光线偏离于光轴的角度。角度越小远心度越好,像就越精确。用来测量远心度的是远心靶板。测试时,测试靶板与光轴成45°放置,这样靶板的底部与顶部距离镜头的远近不同。当通过一个非远心镜头成像时,靶板底部所成的像尺寸会小于顶部所成像的尺寸,这就是梯形畸变。一个完美的远心镜头没有梯形畸变,远心度是0°

普通镜头例f=12mm,相机CCD为1/3″,观察距离S=200mm,高为H=20mm的物体。如果物体由原位置移动了ds=1mm。
则高度值的变化dH=(ds/s).H=(1/200).20mm=0.1mm

远心镜头中,这种比例尺的变化取决于远心度θ。较好的远心镜头远心度为0.1°(1.7mrad)左右。这意味着,在与前面物体同样移动1mm的情况下,测量值只变化了0.0017mm。
三、畸变:高质量的远心镜头通常具有非常低的畸变度,其值在0.1%之内;尽管这个值看起来非常小,但由其导致的测量误差会接近于高分辨率相机一个像素的大小。出于这个原因,在大多数应用中,畸变需要使用软件来校准:将一个精细图案(其几何精度必须至少为所需测量精度的十倍)放置在景深中心;然后在几个像点处计算出畸变,根据这些数据,软件算法可以将原始图像转换成无畸变图像。
畸变不仅取决于光学器件本身,还与被测物体的距离有关;因此,严格遵守额定工作距离是非常重要的。
建议将镜头与被测物体进行精密的垂直校准,这样可以避免非同轴对称畸变效应。梯形畸变(也称为“梯形”或“薄棱镜”效应)是光学检测系统中另一个需要最小化的重要参数,因为它是非对称的,且很难通过软件进行校准。由于机械游隙或光学元件偏离中心,镜头对焦机构也会引入一些对称或非对称的畸变效应。
四、不存在边缘位置不确定性
逆光拍摄物体时,往往很难确定其边缘的确切位置。因为在黑暗的背景下,物体边缘的亮像素往往会与暗像素重叠。此外,如果物体具有高度的三维形状,边界效应也会进一步限制测量精度;如下图所示,光线以一定的入射角掠过物体边缘,被其表面反射后依然会被镜头捕获。镜头由此会认为这些光线来自物体后方;结果部分图像片段可能消失,使得测量非常不精确且不稳定。

如果使用远心镜头,则会大大减少普通成像镜头存在的边界效应。
使用远心镜头可以有效限制这种效应:如果瞳孔孔径足够小,那么可以进入镜头的唯一反射光将是那些近于平行主光轴的光线。
由于这些光线受到非常小的偏差影响,因此物体表面对其的反射不会损害测量精度。
想要完全解决这些问题,可以将准直(也称为“远心”)照明器连接到远心镜头,并利用平行光源发散度处理好镜头孔径与视场的匹配。这样一来,来自照明器的所有光均由镜头收集并传送给探测器,同时可实现极高的信噪比和难以置信的低曝光时间。另一方面,只有“预期的”光线进入成像镜头,这样就不会出现边界问题了。

准直(远心)照明仅将预期光线投射到成像系统中。
更大的景深
景深是物体从最佳焦点位置偏移的最大可接受值。超过这一值,图像分辨率就变得很差,因为来自物体的光线不能在探测器上产生足够小的光斑:光线携带的几何信息分布在太多的图像像素上而产生了模糊效应。景深基本上取决于光学器件的F值,该值与镜头光圈直径成反比:f值越高景深越大,二者拟线性相关。增大F值会降低光锥的发散度,从而允许较小的光斑在探测器上形成;但是F值增大到一定值时会引起衍射效应,从而限制了最大可达到的分辨率。
当拍摄很厚的物体时,双远心度在获得良好图像对比度方面很有优势:光学系统的对称性以及光线的平行性促使图像光斑保持对称性,这样可以降低模糊效应。这使得双远心光学器件的景深比非双远心的大20-30%。