NOIP2018 模拟 9.13

【jzoj 5866】指引

(File IO): input:guide.in $ quad $ output:guide.out Time Limits: 500 ms $ quad $ Memory Limits: 524288 KB Detailed Limits

Description

Input

从文件guide.in中读取数据。
第一行一个整数 $ Num $ ，表示测试点编号，以便选手方便地获得部分分，
你可能不需要用到这些信息，样例中 $ Num $ 地含义为数据范围与某个测试点相同。
接下来一行一个整数 $ N $ ，含义见题目描述。
接下来 $ N $ 行，每行两个整数 $ A_i, B_i $ ，表示每一名旅者的坐标。
接下来 $ N $ 行，每行两个整数 $ C_i, D_i $ ，表示每一个出口的坐标。

Output

一行一个整数，表示答案。

Sample Input

 6 
 3 
 2 0 
 3 1 
 1 3 
 4 2 
 0 4 
 5 5

Sample Output

 2

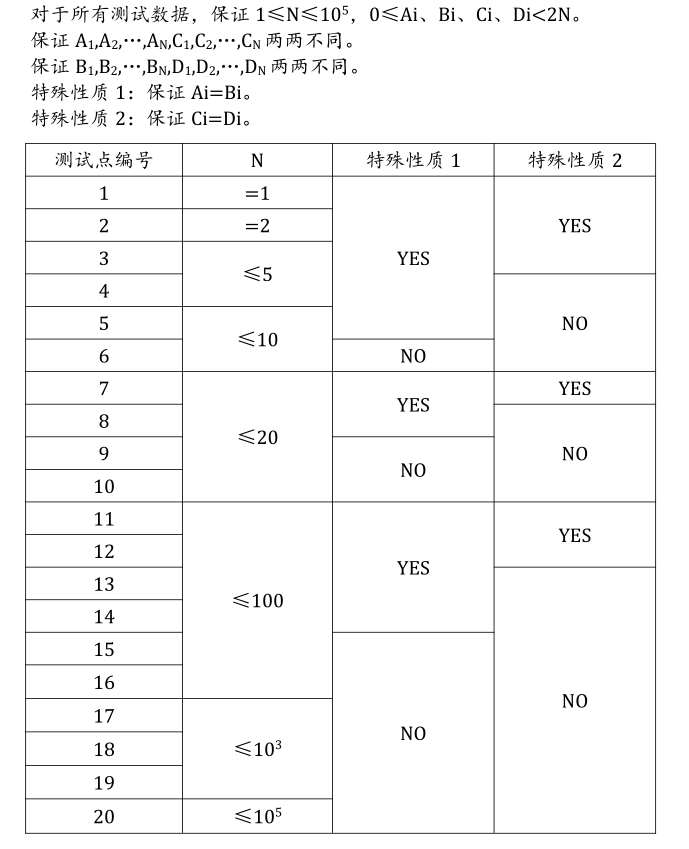
Data Constraint

Hint

【样例1解释】
让位于 $ (2,0) $ 的旅者走到 $ (4,2) $ 处，
让位于 $ (3,1) $ 的旅者走到 $ (5,5) $ 处。

题解

贪心 把所有人按 $ x $ 坐标从大到小排序
每次扫到一个值时，如果是出口，则将一个权值为 $ y $ 的数加入到数据结构里
如果是旅者，则将数据结构中最小的数取出，并且 $ ans++ $
可以用 std：：set 或者线段树、树状数组等维护

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 100005
void read(int &x){
	char ch;x=0;
	while(ch=getchar(),ch<'0'||ch>'9');x=ch-48;
	while(ch=getchar(),ch>='0'&&ch<='9')x=10*x+ch-48;
}
struct node{ int a,b,p; }p[N<<1];
bool cmp(node x,node y){ return x.a>y.a||(x.a==y.a&&x.b<y.b)||(x.a==y.a&&x.b==y.b&&x.p<y.p); }
int num,n,m,ans,maxm;
int sum[N<<3];
void update(int o,int l,int r,int pos){
	++sum[o];
	if(l==r) return; 
	int mid=l+r>>1;
	if(pos<=mid) update(o<<1,l,mid,pos);
	else update(o<<1|1,mid+1,r,pos);
}
bool query(int o,int l,int r,int pos){
	if(sum[o]==0||l>pos) return 0;
	if(l==r){
		--sum[o];
		return 1;
	}
	int mid=l+r>>1;
	if(query(o<<1|1,mid+1,r,pos)){ --sum[o]; return 1; }
	if(query(o<<1,l,mid,pos)){ --sum[o]; return 1; }
	return 0;
}
int main(){
	freopen("guide.in","r",stdin);
	freopen("guide.out","w",stdout);
	read(num);
	read(n); m=(n<<1);
	for(int i=1;i<=n;++i){ 
		read(p[i].a); read(p[i].b); 
		p[i].p=1; p[i].b=m-p[i].b; 
	}
	for(int i=1;i<=n;++i){ 
		read(p[n+i].a); read(p[n+i].b); 
		p[n+i].p=2; p[n+i].b=m-p[n+i].b; 
	}
	sort(p+1,p+1+m,cmp);
	for(int i=1;i<=m;++i)
		if(p[i].p==1){
			if(query(1,1,m,p[i].b)) ++ans;
		} else update(1,1,m,p[i].b);
	printf("%d",ans);
	return 0;
}

---

【jzoj 5867】碎片

(File IO): input:fragment.in $ quad $ output:fragment.out Time Limits: 500 ms $ quad $ Memory Limits: 524288 KB Detailed Limits

Description

小 $ X $ 的记忆中，有一幅 $ N imes M $ 的中心对称的图案。
而现在，他的脑海中只有一幅有所变动的图案，它同样是 $ N imes M $ 的，但却不一定是中心对称的。
小 $ X $ 决定修补这一图案，他能够进行的操作共有两种：交换两行或者交换两列。
小 $ X $ 想知道能否通过有限（可能为0）次操作让它变得中心对称。
为了保证数据的强度，一个测试点中可能包含多组测试数据。

Input

从文件 fragment.in 中读取数据。
第一行两个整数 $ Num, T $ ，
$ Num $ 表示测试点编号，以便选手方便地获得部分分，
你可能不需要用到这则信息，样例中 $ Num $ 的含义为数据范围与某个测试点相同；
$ T $ 表示该测试点中包含的测试数据的组数。
对于接下来每一组测试数据，第一行两个整数 $ N, M $ ，表示图案的大小。
接下来的一个 $ N $ 行 $ M $ 列的字符矩阵，表示图案。

Output

输出 $ T $ 行，每行一个 YES 或 NO ，表示是否能够使图案中心对称。

Sample Input

 6 1 
 2 3  
 ABC 
 BAC

Sample Output

 YES

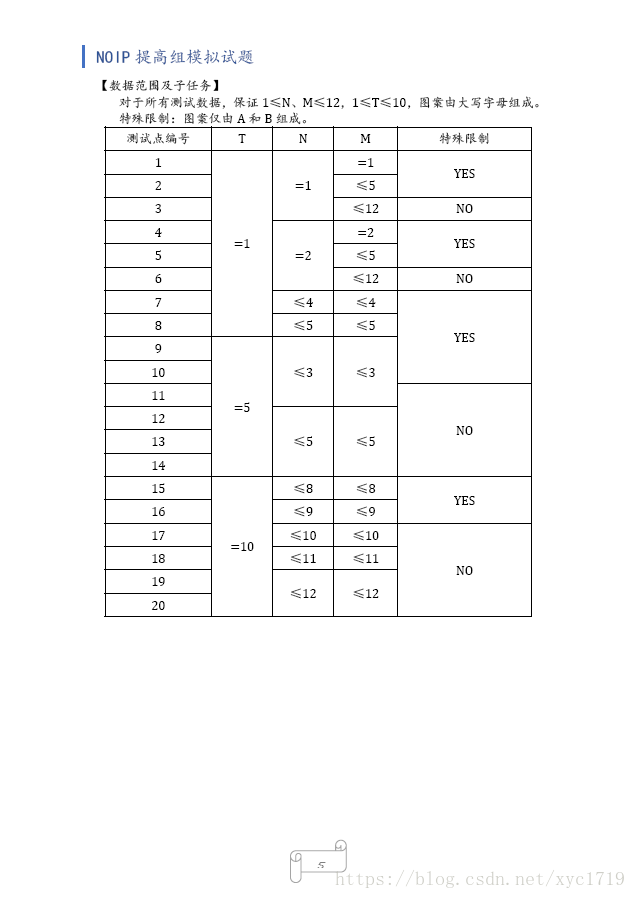
Data Constraint

Hint

【样例1解释】
交换第2列和第3列，得到以下图案：

 ACB
 BCA

它是中心对称的。

题解

有一个很显然的性质，每一行每一列的元素组成都是不变的
所以我们先暴力每一行的情况，利用这一性质剪枝，也就是每一行与其相对的行的元素组成是相同的
然后判断列是否满足
（详情见 XYX 博客）

有如下观察：
1、同一行/列的元素（可重）集合不变。
2、允许任意交换意味着我们可以随意排列行、列的顺序。
3、对称的两行/列元素（可重）集合相同。
4、对于已有的一个可行解，若其两组对称的行/列为 A 和 A′、B 和 B′
那么我们交换 A 和 B，A′ 和 B′ 后，它依然是一组合法解。

考虑枚举。
若 N 为奇数，那么我们就先枚举中间的一行/列对应原矩阵的哪一行/列，这样， 剩余的行/列数变成了偶数。
考虑一次枚举对称的两行/列分别对应原矩阵的哪一行/列，
由观察 4，我们不妨任取一个没 有被选取过的行/列，再枚举一个与之对称的行/列。
对于单次对行/列的排列的枚举，至多有 M=11!!=1197531=10395 种可能的情况。
考虑预处理出每两行/列元素（可重）集合是否相同，并利用观察 3 进行剪枝。
直接枚举行和列的最终排列，并暴力判断方案的合法性，时间复杂度 O(HWM^2)。
但由于利用观察 3 进行的剪枝，无解的情况 M 都只会在在很小的范围内，
而有解的情况在 M 较大时往往情况简单（例如所有元素均相同），很容易就能够找到一组解，并结束搜索，
因此，该算法的实际运行效率甚至比正解更好（最慢 2ms），以下代码实现了该算法。
正解的做法是先枚举行的最终排列，然后将列两两匹配，若能够剩余不足两列（一列或零列）， 那么就找到了一组解。
时间复杂度 O(HW^2M)或 O(HWLogW*M)。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
void read(int &x){
	char ch;x=0;
	while(ch=getchar(),ch<'0'||ch>'9');x=ch-48;
	while(ch=getchar(),ch>='0'&&ch<='9')x=10*x+ch-48;
}
char mp[15][15],x[15],y[15];
int num,T,n,m,Hnum[15],Lnum[15];
bool ans,visL[15],visH[15],L[15][15],H[15][15];
void check(){
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m;++j)
			if(mp[Hnum[i]][Lnum[j]]!=mp[Hnum[n+1-i]][Lnum[m+1-j]]) return;
	ans=1;
	return;
}
void dfsL(int pos,int p){
	if(ans) return;
	if(pos==0){
		check();
		return;
	}
	if(p){
		for(int i=1;i<=m;++i){
			visL[i]=1;
			Lnum[pos]=i;
			dfsL(pos-1,0);
			visL[i]=0;
		}
	} else {
		for(int i=1;i<=m;++i)
			if(!visL[i]){
				for(int j=i+1;j<=m;++j)
					if(!visL[j]&&L[i][j]){
						visL[i]=1;
						visL[j]=1;
						Lnum[pos]=i;
						Lnum[m+1-pos]=j;
						dfsL(pos-1,0);
						visL[i]=0;
						visL[j]=0;
					}
			}
	}
	return;
}
void dfsH(int pos,int p){
	if(ans) return;
	if(pos==0){
		dfsL((m+1)/2,m&1);
		return;
	}
	if(p){
		for(int i=1;i<=n;++i){
			visH[i]=1;
			Hnum[pos]=i;
			dfsH(pos-1,0);
			visH[i]=0;
		}
	} else {
		for(int i=1;i<=n;++i)
			if(!visH[i]){
				for(int j=i+1;j<=n;++j)
					if(!visH[j]&&H[i][j]){
						visH[i]=1;
						visH[j]=1;
						Hnum[pos]=i;
						Hnum[n+1-pos]=j;
						dfsH(pos-1,0);
						visH[i]=0;
						visH[j]=0;
					}
			}
	}
	return;
}
int main(){
	freopen("fragment.in","r",stdin);
	freopen("fragment.out","w",stdout);
	read(num); read(T);
	while(T--){
		read(n); read(m);
		for(int i=1;i<=n;++i) scanf("%s",mp[i]+1);
		for(int i=1;i<=n;++i)
			for(int j=1;j<=n;++j){
				for(int k=1;k<=m;++k){
					x[k]=mp[i][k];
					y[k]=mp[j][k];
				}
				sort(x+1,x+1+m);
				sort(y+1,y+1+m);
				H[i][j]=1;
				for(int k=1;k<=m;++k)
					if(x[k]!=y[k]) H[i][j]=0;
			}
		for(int i=1;i<=m;++i)
			for(int j=1;j<=m;++j){
				for(int k=1;k<=n;++k){
					x[k]=mp[k][i];
					y[k]=mp[k][j];
				}
				sort(x+1,x+1+n);
				sort(y+1,y+1+n);
				L[i][j]=1;
				for(int k=1;k<=n;++k)
					if(x[k]!=y[k]) L[i][j]=0;
			}
		ans=0;
		dfsH((n+1)/2,n&1);
		if(!ans) puts("NO");
		else puts("YES");
	}
	return 0;
}

---