$ Rightarrow $ 戳我看题面PDF$ Rightarrow $ 戳我看题解PDF$ Rightarrow $ 戳我下载数据包
计数
时间限制:1s
内存限制:256MB
【问题描述】
给出 $ m $ 个数 $ a[1],a[2],…,a[m] $
求 $ 1~n $ 中有多少数不是 $ a[1],a[2],…,a[m] $ 的倍数。
【输入】
输入文件名为 $ count.in $ 。
第一行,包含两个整数:$ n,m $
第二行,包含 $ m $ 个数,表示 $ a[1],a[2],…,a[m] $
【输出】
输出文件名为 $ count.out $ 。
输出一行,包含 $ 1 $ 个整数,表示答案
【输入输出样例】
count.in
10 2
2 3
count.out
3
【数据说明】
对于 $ 60 $ %的数据,$ 1 le n le 10^6 $ 对于
另外 $ 20 $ %的数据,$ m=2 $
对于 $ 100 $ %的数据,$ 1 le n le 10^9,0<m le 20,1 le a[i] le 10^9 $
【题解】
容斥原理即可
时间复杂度 $ O(2^m imes log) $
【代码】
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
inline int read() {
register char ch;
while(!isdigit(ch=getchar()));
register int x=ch^'0';
while(isdigit(ch=getchar())) x=(((x<<2)+x)<<1)+(ch^'0');
return x;
}
inline void write(int a){
if(a<0)putchar('-'),a=-a;
register int top=0,q[20];
while(a)q[++top]=a%10,a/=10;
top=max(top,1ll);
while(top--)putchar('0'+q[top+1]);
puts("");
}
int n,m,a[21],ans;
int gcd(int x,int y){ return y==0 ? x : gcd(y,x%y); }
void dfs(int step,int k,int lcm){
//step为选到第几个数,选了k个数,它们的最小公倍数为lcm
if(lcm>n) return;
if(step==m+1){
if(k&1) ans-=n/lcm;
else ans+=n/lcm;
//如果选完了,选了偶数个数,这些数的贡献一定被重复计算了,减去这些贡献
//而选了奇数个时,它们的贡献又被删重复了,它们的贡献将会被加回
return;
}
dfs(step+1,k+1,lcm*a[step]/gcd(lcm,a[step]));
//枚举所有数字可能组合的最小公倍数
dfs(step+1,k,lcm);
}
signed main(){
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
n=read(); m=read();
for(int i=1;i<=m;++i) a[i]=read();
dfs(1,0,1);
write(ans);
return 0;
}
区间第 k 大
时间限制:1s
内存限制:256MB
【问题描述】
一个区间的价值定义为该区间中的最大值减最小值
给定 $ n $ 个数,求所有区间价值中,第 $ k $ 大值为多少。
【输入】
输入文件名为 $ kth.in $。
第 1 行两个数 $ n、k(k le n imes (n-1)/2) $
第 2 行 $ n $ 个数,每个数 $ le 10^9 $
【输出】
输出文件名为 $ kth.out $。
输出区间价值的第 $ k $ 大值。
【输入输出样例】
kth.in
3 2
2 1 3
kth.out
2
【样例解释】
$ [l,r] $ 表示第 $ i $ 个数到第 $ r $ 个数组成的区间的价值
$ [1,1]=0 quad [1,2]=1 quad [1,3]=2 (
) [2,2]=0 quad [2,3]=2 $
$ [3,3]=0 $
【数据说明】
对于 $ 30 $ %的数据,$ n=500 $
对于 $ 60 $ %的数据,$ n le 5000 $
对于 $ 100 $ %的数据,$ n le 400000 $
【题解】
-
对于 $ 30 $ %的数据:
-
求出每个区间的价值,然后排序
-
时间复杂度 $ O(n^2 imes log^2_n) $
-
对于 60%的数据:
-
对于 30%的做法中,在 m 个元素中寻找第 k 大可以在快排中做到 O(m)
-
时间复杂度 $ O(n^2) $
-
对于 $ 100 $%的数据:
-
二分答案 $ ans $ ,统计有多少个区间的价值大于等于 $ ans $
-
区间 $ [l-1,r] $ 的价值一定大于等于 $ [l,r] $ 所以对于每一右端点 $ i $,
必定存在一个阀值 $ K_i $ 使得对于所有的 $ l<=Ki[l,i] $ 的价值必定大于等于 $ ans $ -
且随之 $ i $ 的增大,$ K_i $ 也必定单调不降
-
用两个单调队列来维护阀值 $ K $ 的移动
(一个维护最小值,一个维护最大值,当 $ K $ 增加时判 定最大值-最小值是否大于等于 $ ans $ 即可) -
时间复杂度 $ O(log_210^9 imes n) $
【代码】
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define int long long
#define N 400005
inline int read() {
register char ch;
while(!isdigit(ch=getchar()));
register int x=ch^'0';
while(isdigit(ch=getchar())) x=(((x<<2)+x)<<1)+(ch^'0');
return x;
}
inline void write(int a){
if(a<0)putchar('-'),a=-a;
register int top=0,q[20];
while(a)q[++top]=a%10,a/=10;
top=max(top,1ll);
while(top--)putchar('0'+q[top+1]);
puts("");
}
int n,k,a[N],qmx[N],qmn[N],ans,maxa;
bool check(int x){
int l1=1,r1=1,l2=1,r2=1,p1,p2,p=1,res= x==1 ? 1 : 0;
qmx[l1]=qmn[l2]=1;
for(int i=2;i<=n;++i){
while(l1<=r1&&a[qmx[r1]]<a[i]) --r1; qmx[++r1]=i;
while(l2<=r2&&a[qmn[r2]]>a[i]) --r2; qmn[++r2]=i;
while(p<i){
p1=l1; p2=l2; ++p;
while(qmx[p1]<p) ++p1;
while(qmn[p2]<p) ++p2;
if(a[qmx[p1]]-a[qmn[p2]]>=x){ l1=p1; l2=p2; }
else{ --p; break; }
}
if(a[qmx[l1]]-a[qmn[l2]]>=x) res+=p;
}
return res>=k;
}
signed main(){
freopen("kth.in","r",stdin);
freopen("kth.out","w",stdout);
n=read(); k=read();
for(int i=1;i<=n;++i){
a[i]=read();
maxa=maxa>a[i] ? maxa : a[i];
}
int l=0,r=maxa,mid;
while(l<=r) check(l+r>>1) ? ans=l+r>>1,l=(l+r>>1)+1 : r=(l+r>>1)-1;
write(ans);
return 0;
}
武器分配
时间限制:1s
内存限制:256MB
【问题描述】
有 $ n $ 个堡垒排成一排构成了一条防御线。
现在需要将 $ n $ 个武器放入这 $ n $ 个堡垒中,每个堡垒放一个,每个武器有攻击力和战场贡献值两个属性。
由于这 $ n $ 个武器都不是人为操控的,所以会对其某半径内所有单位进行攻击,而这就导 致某些堡垒的互相攻击。
现在发现第 $ i $ 个堡垒会和第 $ j $ 个堡垒互相攻击当且仅当 $ |i-j|<=r $ , 且攻击力较低的武器和他所在的堡垒会破损。
现在你需要给出一种武器分配方案使得未破损武器的战场贡献值总和最大。
为了方便,你只需输出战场贡献值总和的最大值即可。
【输入】
输入文件名为 $ submax.in $ 。
第一行一个数 $ T(le 10) $ ,表示数据组数
对于每一组数据:
第一行两个数 $ n,r $
第二行 $ n $ 个数,表示 $ 1~n $ 号武器的攻击力
第三行 $ n $ 个数,表示 $ 1~n $ 号武器的战场贡献值
【输出】
输出文件名为 $ submax.out $ 。
对于每组数据输出一个数,表示答案
【输入输出样例】
submax.in
1
4 2
1 2 3 4
1 2 3 4
submax.out
7
【题解】
-
对于 $ 30 $ %的数据:
-
$ n! $ 枚举即可
-
时间复杂度 $ O(n! imes n) $
-
对于 $ 60 $ %的数据:
-
考虑按照攻击力从大到小放置武器,用二进制状态 $ k $ 表示每个堡垒是否放入了武器。
-
根据二进制状态 $ 1 $ 的个数可算出下一个应该放哪一武器,再 $ O(n) $ 转移即可。
-
对于 $ 100 $ %的数据:
-
考虑如果选定了几个武器要求这些武器都不被摧毁,判断是否可能
-
按照攻击力从小到大把每个选定的武器放入,每放入一个选定的武器后在其后面添加 r 个比他攻击力小的武器,
若当前找不出 r 个比它攻击力小的武器则判断失败 -
如图,选定 $ 3 $ 号、$ 6 $ 号武器,即可通过如下方式进行构造
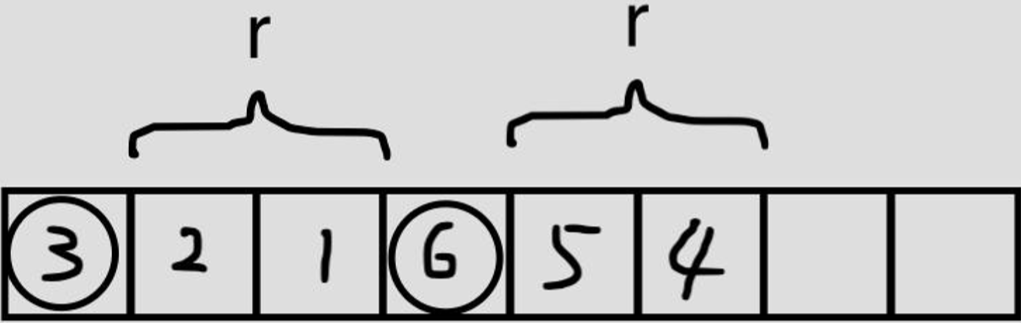
-
以上判断有个简单的表示方式:
攻击力第 $ i $ 小的选定武器其攻击力在所有武器中的排名需 要 $ ge i imes (r+1) $ -
需要注意的是,如果最后放入的选定武器是攻击力最大的武器则不需要这个判断所以,
可以按照攻击力从小到达把所有武器排序,$ dp[i][j] $ 表示前 $ j $ 个武器选了 $ i $ 个且判定合法的战场贡献最大值 -
$ dp[i][1~(r+1) imes i -1]=-INF $
-
$ f[i][j]=max(dp[i][k])=max(dp[i][j],f[i][j-1]),k<j $
-
$ dp[i][j]=max(dp[i-1][k])+contribution[j]=f[i-1][j-1]+contribution[j],k<j $
-
在所有 $ dp[i][j] $ 中取最大值即为答案
【代码】
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define int long long
#define INF 4e18
#define N 5005
inline int read() {
register char ch;
while(!isdigit(ch=getchar()));
register int x=ch^'0';
while(isdigit(ch=getchar())) x=(((x<<2)+x)<<1)+(ch^'0');
return x;
}
inline void write(int a){
if(a<0)putchar('-'),a=-a;
register int top=0,q[20];
while(a)q[++top]=a%10,a/=10;
top=max(top,1ll);
while(top--)putchar('0'+q[top+1]);
puts("");
}
int n,r,T,ans;
struct weapon{ int atk,val; }w[N];
int f[N][N];
bool cmp(weapon x,weapon y){ return x.atk<y.atk; }
signed main(){
freopen("submax.in","r",stdin);
freopen("submax.out","w",stdout);
T=read();
while(T--){
ans=0;
n=read(); r=read();
for(int i=1;i<=n;++i) w[i].atk=read();
for(int i=1;i<=n;++i) w[i].val=read();
sort(w+1,w+1+n,cmp);
int m=(n-1)/(r+1)+1;
for(int i=1;i<=m;++i){
int p=min(i*(r+1),n);
for(int j=0;j<p;++j) f[i][j]=-INF;
for(int j=p;j<=n;++j) f[i][j]=w[j].val+f[i-1][j-1];
for(int j=1;j<=n;++j) f[i][j]=max(f[i][j],f[i][j-1]);
ans=max(ans,f[i][n]);
}
write(ans);
}
return 0;
}