FROM:

说明,开销单位
32-bit XOR = 80 GE, 32-bit arithmetic ADD = 148 GE,
192-bit FF = 1344 GE, SHIFT = 0 GE
SP-network
31 rounds
Ki i={1,2, ... , 32} k32用来做白化(线性的置换和非线性的替换) 由user-supplied key来生成
The block length is 64 bits
key lengths of 80 or 128 bits
很多时候用80bits是可行的,也符合eSTREAM项目中面向硬件的流密码的设计目标
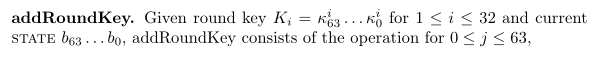


子密钥Ki是当前密钥寄存器中最左边的64位 对应
κ63 κ62 ... κ0 = Ki (子密钥)
k79 k78 ... k16 = K(密钥寄存器)
每当提取完轮密钥 κi 后,密钥寄存器做更新:
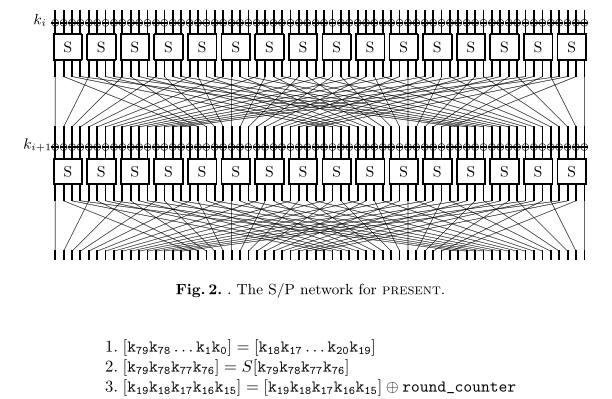
除了安全和高效实现之外,设计present时的主要目标是简单。因此,类似的设计被考虑到[21]的其他环境中,甚至可以用作学生[20]的教程,这并不奇怪。在本节中,我们将说明我们在设计present时所做的决定。然而,首先,我们描述预期的应用程序需求。
使用目标和环境
并不是要广泛使用(来替代)已经存在的密钥(如AES),而是在一些不适合使用AES的情况下,常有这t样的特征:
密码吗要在硬件上实现
Applications只需要中等安全级别
Applications不太可能需要对大量数据加密
对于一些设备可以在制造的时候就把密钥固定,而不是由用户自己进行密钥的重置 (对安全性来说是优的)
安全性+实现的物理空间+峰值+平均功耗+定时需求
空间的最有效使用--分组密码只用来加密 (?)
即


由于这些因素,所以设计者决定使用64-bits 的分组密码(带有80-bits 的密钥长度)
使得加密解密有大致相同的物理要求
选择同时支持加密和解密将产生一个轻量级块密码实现,它仍然比encryption-only AES小。

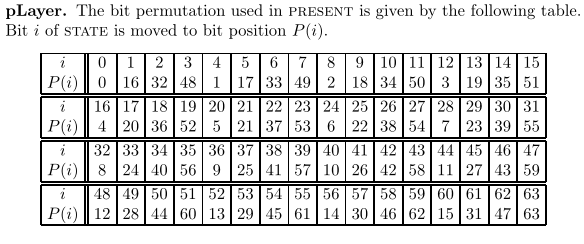
The permutation layer(置换层) 也叫线形层
主要关注硬件效率,使用最少数量的处理元件 ========> bit permutation n
The S-box S盒

为的就是比六位8位的S盒更compact 更有效率一些
对S盒的雪崩效应做改善:数学描述

正如在第5节中将变得清楚的那样,这些条件将确保present抵抗微分和线性攻击。通过对满足上述条件
的所有4位S-box进行分类,我们选择了一个特别适合于高效硬件实现的S-box
安全性分析
1、差分、线性密码分析
为了描述Present对差分、线性密码分析的抵抗性,提供一个涉及到微分(或线性)特性的所谓动态s盒数量的下界。



给出一些相关Theorem
4轮PERESENT的线性逼近表达式的最大偏差为 $varepsilon_{4} = frac{1}{2^7}$ 可以证明。然后用它来确定28轮线性逼近表达式的最大偏差:
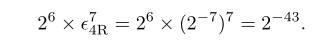 (堆积引理得到的结果)
(堆积引理得到的结果)
所以在这样的假设下,分析者需要近似31轮的28轮就可以恢复密钥攻击,线性密码分析要求大概要$2^84$个明文/密文对 显然不现实
Structural attacks such as integral attacks [25] and bottleneck attacks [17] are well-
suited to the analysis of AES-like ciphers
很强的词结构,其中的单词通常是字节 but 目前的设计通常是字节
代数攻击用在流密码比用在分组密码更成功
Persent结构简单同时也有研究的意义
目前的S-box由GF(2)上8个输入/输出变量的21个二次方程描述。这并不奇怪,因为众所周知,任何四位S-box都可以用至少21个这样的方程来描述。
整个密码可以用e = n * 21个v = n * 8个变量的二次方程来描述,其中n为加密算法中的s盒数和密钥调度。
目前我们有n =(31×16)+ 31,因此整个系统包含11,067个二次方程,包含4216个变量。
那么问题就是------求解多元二次方程系统的一般问题是np难问题。然而,由于分组密码系统是由n个小系统通过简单的线性层连接而成的,因此其系统非常稀疏。然而,还不清楚这一事实是否可以利用在所谓的代数攻击。
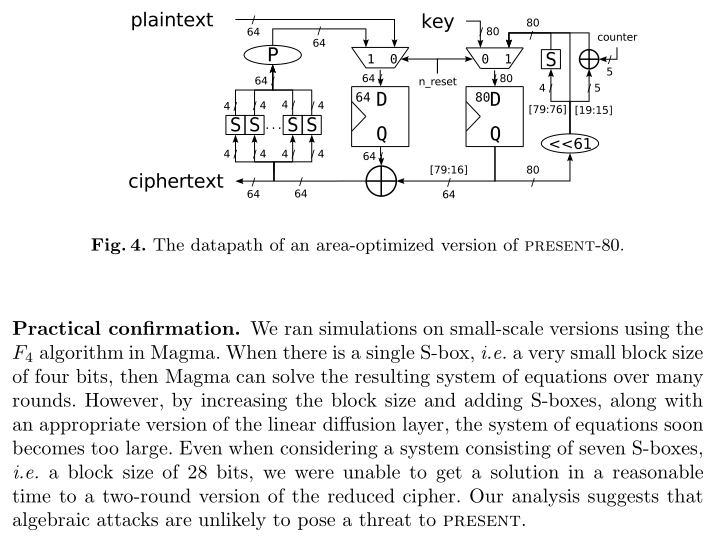
提出PRESENT的人,使用Magma中的f4算法在小规模版本上进行了模拟。当只有一个S-box时,即只有四个比特的非常小的块,岩浆就可以在许多回合中求解得到的方程组。然而,通过增加块大小和增加s盒以及适当的线性扩散层,方程组很快就变得太大了。即使考虑一个由7个s盒组成的系统,即一个28位的块大小,我们也无法在合理的时间内得到一个两轮简化密码版本的解决方案。我们的分析表明,代数攻击不太可能对现在构成威胁。
 ?
?
密钥周期攻击,依赖于不同的子集某种可识别关系
related-key attacks and slide attacks
解决办法,使用一个依赖循环的计数器

本文描述了一种新的分组密码。我们的目标是开发一种超轻量级密码,提供与64位块大小和80位密钥相称的安全级别。有趣的是,present的实现要求类似于许多紧凑流密码。因此,我们认为它具有理论和实际意义。同所有新的建议一样,我们不鼓励立即部署现有的建议,但强烈鼓励对其进行分析。