1.基本思想：
综合某些专家的判断，往往要比一个专家单独的判断要好。在”强可学习”和”弱可学习”的概念上来说就是我们通过对多个弱可学习的算法进行”组合提升或者说是强化”得到一个性能赶超强可学习算法的算法。如何地这些弱算法进行提升是关键！AdaBoost算法是其中的一个代表。
2.分类算法提升的思路：
1.找到一个弱分类器，分类器简单，快捷，易操作(如果它本身就很复杂，而且效果还不错，那么进行提升无疑是锦上添花，增加复杂度，甚至上性能并没有得到提升，具体情况具体而论)。
2.迭代寻找N个最优的分类器(最优的分类器，就是说这N个分类器分别是每一轮迭代中分类误差最小的分类器，并且这N个分类器组合之后是分类效果最优的。)。
在迭代求解最优的过程中我们需要不断地修改数据的权重(AdaBoost中是每一轮迭代得到一个分类结果与正确分类作比较，修改那些错误分类数据的权重，减小正确分类数据的权重 ),后一个分类器根据前一个分类器的结果修改权重在进行分类，因此可以看出，迭代的过程中分类器的效果越来越好，所以需要给每个分类器赋予不同的权重。最终我们得到了N个分类器和每个分类器的权重，那么最终的分类器也得到了。
3.算法流程：(数据默认：M*N,M行N列，M条数据，N维 )
输入：训练数据集,：弱学习算法(xi表示数据i[数据i是个N列/维的],yi表示数据的分类为yi,Y={-1,1}表示xi在某种规则约束下的分类可能为-1或+1)
输出：最终分类器G(x)
1)初始化训练数据的权值分布(初始化的时候每一条数据权重均等)
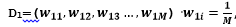,M表示数据的个数，i=1,2,3…M
2)j=1,2,3,…,J(表示迭代的次数/或者最终分类器的个数,取决于是否能够使分类误差为0)
a)使用具有权值分布Dj的训练数据集学习，得到基本的分类器
Gj(x):X->{-1,+1}
b)计算Gj(x)在训练集上的分类误差率
求的是分错类别的数据的权重值和,表示第i个数据的权重Dj[i]
c)计算Gj(x)第j个分类器的系数(权重),ln表示以E为底的自然对数跟ej没什么关系,ej表示的是分类错误率。
d)更新训练数据集的权重Dj+1,数据集的权重是根据上一次权重进行更新的， i=1,2,3…M(xi表示第i条数据)
Z是规范化因子，他表示所有数据权重之和，它使Dj+1成为一个概率分布。
3)构建基本分类器的线性组合
得到最终的分类器：
4.用一组数据来具体解说一下Adaboost的实现过程:
Data：5*2
原始类别：
1.初始化数据权重D1=（1/5,1/5,1/5,1/5,1/5）,五条数据所以是5列，w=1/m
2.分类器
通过计算得到误差率最小时V的值，但是最小误差率是由分类结果G（x）得到的，所以这个V值我们只有通过穷举得到。
1).按第一维度来分类：
我们找到第一维所有数据的极值（min=1,max=2）,我们从最小的数据1开始，每次增加0.5，即V=min+0.5*n,n表示次数。
当v=1+0.5*1=1.5时，
分类结果G(x):
G(x)=[1<1.5->1,2>1.5->-1,1.3<1.5->1,1<1.5->1,2>1.5->-1]
G(x)=[1,-1,1,1,-1]
误差率为e1:
e1=sum(D[G(xi)!=yi])误分类点的权重和
我们来比较一下分类器的分类结果和原始类别就知道那些分错了：
G(x)=[1,-1,1,1,-1]
Lables=[1,1,-1,-1,1]
对比一下可以发现第2，3，4,5都分错了。
e1=D[2]+D[3]+D[4]+D[5]=0.8
交换一下符号：即
分类结果G(x):
G(x)=[1<1.5->-1,2>1.5->1,1.3<1.5->-1,1<1.5->-1,2>1.5->1]
G(x)=[-1,1,-1,-1,1]
误差率为e1:
G(x)=[-1,1,-1,-1,1]
Lables=[1,1,-1,-1,1]
对比一下可以发现第1个错了。
e1=D[1]=0.2
分类器权重alpha:
Alpha = 0.5*ln((1-0.2)/0.2)
更新数据权重D：
sum(D1)=1
D2=((D1[1]*e(-alpha*-1))/sum(D1), (D1[1]*e(-alpha*1))/1,..)
e的系数最后的+-1取决于是否正确分类，分正确了就是1，分错误了就是-1，前面公式中也有写到。
这里的计算公式是统计学习方法中的，跟机器学习实战中的D的计算有一点出入，在机器学习实战中D是这么计算的：
D2= D1[1]*e(-alpha*-1)
D2=D2/sum(D2)
但是就结果而言，好像影响不大，只是对这个加权误差有影响。
我们得到两个分类器：
当v=1+0.5*2=1.5时，
重复以上步骤得到两个分类器。
当v=1+0.5*s时，一共寻找了2s次
当我们从最小值找分类阈值直到最大值时，我们得到了2s个分类器，s表示寻找的次数。我们记录效果最好的分类器即分类误差最小的分类器。那么我们在一个维度上的寻找就完成了。
2).接下来在第二个维度上寻找，同样得到2s个分类器
。。。
3).直到第N维,总共得到N*2s个分类器，最终在这么多分类器找到一个最优的分类器。一次迭代完成。
3.接下来将上面这个过程重复J次(J表示迭代次数，如果h次(h<J)就得到了误差为0的分类器那么提前结束迭代。)
按所给数据，迭代三次就能够找到误差为零的分类器
看到这里应该对整个过程有了一个了解，对于数据权重D和分类器的权重alpha，以及分类误差率e的计算都有了一个了解，看一下代码：
源码：（源码是按照《机器学习实战》来写的，因为个人对于python不太熟，机器学习实战中的代码运用矩阵来做很多公式中的乘法，有很大的技巧性，可能开始看的时候没法理解这样做，需要和理论结合，理论则是是来自《统计学习方法》）
1 # -*- coding:utf-8 -*-
2 # Filename: AdaBoost.py
3 # Author：Ljcx
4
5 """
6 AdaBoost提升算法:(自适应boosting)
7 优点：泛化错误率低，易编码，可以应用在大部分分类器上，无参数调整
8 缺点：对离群点敏感
9
10 bagging:自举汇聚法(bootstrap aggregating)
11 基于数据随机重抽样的分类器构建方法
12 原始数据集中重新选择S次得到S个新数据集，将磨沟算法分别作用于这个数据集,
13 最后进行投票，选择投票最多的类别作为分类类别
14
15 boosting:类似于bagging,多个分类器类型都是相同的
16
17 boosting是关注那些已有分类器错分的数据来获得新的分类器，
18 bagging则是根据已训练的分类器的性能来训练的。
19
20 boosting分类器权重不相等，权重对应与上一轮迭代成功度
21 bagging分类器权重相等
22 """
23 from numpy import*
24
25
26 class Adaboosting(object):
27
28 def loadSimpData(self):
29 datMat = matrix(
30 [[1., 2.1],
31 [2., 1.1],
32 [1.3, 1.],
33 [1., 1.],
34 [2., 1.]])
35 classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
36 return datMat, classLabels
37
38 def stumpClassify(self, datMat, dimen, threshVal, threshIneq):
39 """
40 通过阈值比较进行分类
41 dataMat:数据矩阵
42 dimen:表示列下标
43 threshVal:阈值
44 threshIneq:不等号 lt, gt
45 只是简单的将数据分为两类-1，1，初始化了一个全1的矩阵，我们判断一下阈值第i列小于/大于阈值的就为-1，(因为我们并不清楚这个划分标准，所以要大于小于都试一次)
46
47 每一个维度的所有数据跟阈值比较，就相当于找到一个点划分所有数据。
48
49 """
50 # print "-----data-----"
51 # print datMat
52 retArr = ones((shape(datMat)[0], 1)) # m(数据量)行，1列，列向量
53 if threshIneq == 'lt':
54 retArr[datMat[:, dimen] <= threshVal] = -1.0 # 小于阈值的列都为-1
55 else:
56 retArr[datMat[:, dimen] > threshVal] = -1.0 # 大于阈值的列都为-1
57 # print "---------retArr------------"
58 # print retArr
59 return retArr
60
61 def buildStump(self, dataArr, classLables, D):
62 """
63 单层决策树生成函数
64 """
65 dataMatrix = mat(dataArr)
66 lableMat = mat(classLables).T
67 m, n = shape(dataMatrix)
68 numSteps = 10.0 # 步数，影响的是迭代次数，步长
69 bestStump = {} # 存储分类器的信息
70 bestClassEst = mat(zeros((m, 1))) # 最好的分类器
71 minError = inf # 迭代寻找最小错误率
72 for i in range(n):
73 # 求出每一列数据的最大最小值计算步长
74 rangeMin = dataMatrix[:, i].min()
75 rangeMax = dataMatrix[:, i].max()
76 stepSize = (rangeMax - rangeMin) / numSteps
77 # j唯一的作用用步数去生成阈值，从最小值大最大值都与数据比较一边了一遍
78 for j in range(-1, int(numSteps) + 1):
79 threshVal = rangeMin + float(j) * stepSize # 阈值
80 for inequal in ['lt', 'gt']:
81 predictedVals = self.stumpClassify(
82 dataMatrix, i, threshVal, inequal)
83 errArr = mat(ones((m, 1)))
84 errArr[predictedVals == lableMat] = 0 # 为1的 表示i分错的
85 weightedError = D.T * errArr # 分错的个数*权重(开始权重=1/M行)
86 # print "split: dim %d, thresh %.2f, thresh ineqal:
87 #%s,the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
88 if weightedError < minError: # 寻找最小的加权错误率然后保存当前的信息
89 minError = weightedError
90 bestClassEst = predictedVals.copy() # 分类结果
91 bestStump['dim'] = i
92 bestStump['thresh'] = threshVal
93 bestStump['ineq'] = inequal
94 # print bestStump
95 # print minError
96 # print bestClassEst # 类别估计
97 return bestStump, minError, bestClassEst
98
99 def adaBoostingDs(self, dataArr, classLables, numIt=40):
100 """
101 基于单层决策树的AdaBoosting训练过程：
102 """
103 weakClassArr = [] # 最佳决策树数组
104 m = shape(dataArr)[0]
105 D = mat(ones((m, 1)) / m)
106 aggClassEst = mat(zeros((m, 1)))
107 for i in range(numIt):
108 bestStump, minError, bestClassEst = self.buildStump(
109 dataArr, classLables, D)
110 print "bestStump:", bestStump
111 print "D:", D.T
112 alpha = float(
113 0.5 * log((1.0 - minError) / max(minError, 1e-16)))
114 bestStump['alpha'] = alpha
115 weakClassArr.append(bestStump)
116 print "alpha:", alpha
117 print "classEst:", bestClassEst.T # 类别估计
118
119 expon = multiply(-1 * alpha * mat(classLables).T, bestClassEst)
120 D = multiply(D, exp(expon))
121 D = D / D.sum()
122
123 aggClassEst += alpha * bestClassEst
124 print "aggClassEst ；", aggClassEst.T
125 # 累加错误率
126 aggErrors = multiply(sign(aggClassEst) !=
127 mat(classLables).T, ones((m, 1)))
128 # 错误率平均值
129 errorsRate = aggErrors.sum() / m
130 print "total error:", errorsRate, "
"
131 if errorsRate == 0.0:
132 break
133 print "weakClassArr:", weakClassArr
134 return weakClassArr
135
136 def adClassify(self, datToClass, classifierArr):
137 """
138 预测分类：
139 datToClass：待分类数据
140 classifierArr: 训练好的分类器数组
141 """
142 dataMatrix = mat(datToClass)
143 m = shape(dataMatrix)[0]
144 aggClassEst = mat(zeros((m, 1)))
145 print
146 for i in range(len(classifierArr)): # 有多少个分类器迭代多少次
147 # 调用第一个分类器进行分类
148 classEst = self.stumpClassify(dataMatrix, classifierArr[i]['dim'],
149 classifierArr[i]['thresh'],
150 classifierArr[i]['ineq']
151 )
152 # alpha 表示每个分类器的权重，
153 print classEst
154 aggClassEst += classifierArr[i]['alpha'] * classEst
155 print aggClassEst
156 return sign(aggClassEst)
157
158
159 if __name__ == "__main__":
160 adaboosting = Adaboosting()
161 D = mat(ones((5, 1)) / 5)
162 dataMat, lableMat = adaboosting.loadSimpData()
163 # 训练分类器
164 classifierArr = adaboosting.adaBoostingDs(dataMat, lableMat, 40)
165 # 预测数据
166 result = adaboosting.adClassify([0, 0], classifierArr)
167 print result
运行结果：可以看到迭代三次加权错误率为0
最后有一个对数据[0,0]的预测：weakClassArr表示保存的三个分类器的信息，我们用这个分类器对数据进行预测
三个小数对应的是三个分类器前N个分类加权分类结果累加。对应的-1，-1，-1表示三个分类器对这个数据分类是-1，最后一个表示增强分类器对这个数据的加权求和分类结果为-1