【51NOD1494】选举拉票

题面

现在你要竞选一个县的县长。你去对每一个选民进行了调查。你已经知道每一个人要选的人是谁，以及要花多少钱才能让这个人选你。现在你想要花最少的钱使得你当上县长。你当选的条件是你的票数比任何一个其它候选人的多（严格的多，不能和他们中最多的相等）。请计算一下最少要花多少钱。1 ≤ n ≤ 10^5，0 ≤ ai ≤ 10^5; 0 ≤ bi ≤ 10^4

分析

选举拉票是否违法？

是否违法要根据具体行为来判断，比如通过做好人好事这种方式是不违法的，但使用金钱贿赂选民这是违法的。相关法律如下：

《中华人民共合国选举法》第五十七条

为保障选民和代表自由行使选举权和被选举权，对有下列行为之一，破坏选举，违反治安管理规定的，依法给予治安管理处罚；构成犯罪的，依法追究刑事责任：
（一）以金钱或者其他财物贿赂选民或者代表，妨害选民和代表自由行使选举权和被选举权的；
（二）以暴力、威胁、欺骗或者其他非法手段妨害选民和代表自由行使选举权和被选举权的；

（三）伪造选举文件、虚报选举票数或者有其他违法行为的；

（四）对于控告、检举选举中违法行为的人，或者对于提出要求罢免代表的人进行压制、报复的。

国家工作人员有前款所列行为的，还应当依法给予行政处分。以本条第一款所列违法行为当选的，其当选无效

好了不皮了

值域线段树+扫描线思想。

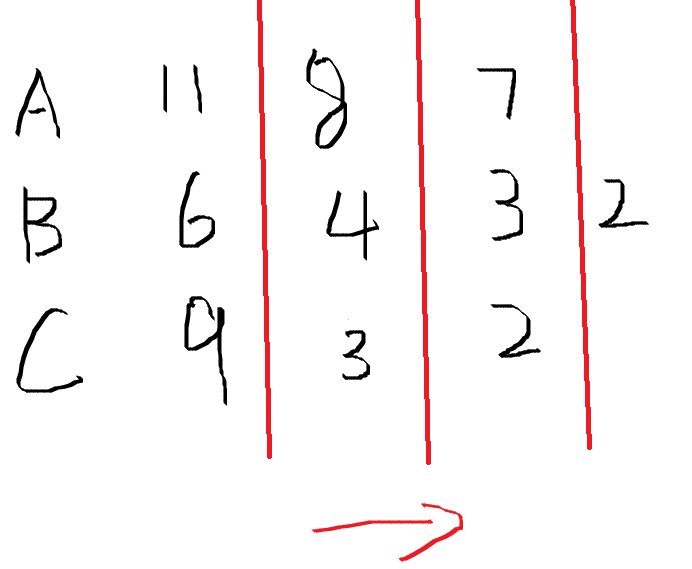
姑且把这红色的线认为是扫描线。对于每个参选人得到的票，我们按照收买投票的价格从大到小排序，然后在将这些收买的人分为mxb个梯队，此图mxb==4

枚举这个人需要买多少张票是比较困难的，因为买到别人的票过后，你实际需要的票可能也减少了，会很多无效和不合理的枚举。

因此我们枚举给其他参选人留多少张票，即留下多少个梯队i。而我们只需要i+1张选票即可。

每次，留下的梯队增加，代表红线右移，同时将红线左边元素全部加入线段树。

红线右边的票是代表全部买的，红线左边的票仅在右边的票不足i+1张时，选其中最小的前几张买，补足i+1即可。

维护前几小的和，用值域线段树。

代码

#include<bits/stdc++.h>
using namespace std;
#define N 100010
#define lc (p<<1)
#define rc (p<<1|1)
#define mid (t[p].l+t[p].r>>1)
int a,b,n,k,del,tmp,mxa,mxc,res,ans,mxb=1;
vector<int>vb[N];
vector<int>vc[N];
struct email
{
    int l,r,num,sum;
}t[N*4];
inline void pushup(int p)
{
    t[p].num=t[lc].num+t[rc].num;
    t[p].sum=t[lc].sum+t[rc].sum;
}

inline void build(int p,int l,int r)
{
    t[p].l=l;t[p].r=r;
    if(l==r)return;
    int bm=l+r>>1;
    build(lc,l,bm);build(rc,bm+1,r);
}

inline void update(int p,int x)
{
    if(t[p].l==t[p].r)
    {
        t[p].num++;
        t[p].sum+=t[p].l;
        return ;
    }
    if(x<=mid)update(lc,x);
    if(x>mid)update(rc,x);
    pushup(p);
}
inline int query(int p,int cnt)
{
    if(t[p].l==t[p].r)return t[p].l*cnt;
    if(cnt==t[lc].num) return t[lc].sum; 
    if(cnt>t[lc].num)return t[lc].sum+query(rc,cnt-t[lc].num);
    if(cnt<t[lc].num)return query(lc,cnt);
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&a,&b);
        if(b==0)continue;
        mxa=max(mxa,a);mxb=max(mxb,b);
        ans+=b;
        vb[a].push_back(b);
    }
    for(int i=1;i<=mxa;i++)
    {
        sort(vb[i].begin(),vb[i].end(),greater<int>());
        mxc=max(mxc,(int)vb[i].size());
        for(int j=0;j<vb[i].size();j++)
            vc[j].push_back(vb[i][j]);
    }
    k=n,res=ans;
    build(1,1,mxb);
    for(int i=0;i<mxc;i++)
    {
        k-=vc[i].size();
        for(int j=0;j<vc[i].size();j++)
        {
            update(1,vc[i][j]);
            res-=vc[i][j];
        }
        tmp=0;
        if(k<=i+1)
        {
            del=min(i+2-k,n);
            tmp=query(1,del);
        }
        ans=min(ans,res+tmp);
    }
    printf("%d
",ans);
    return 0;
}