给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
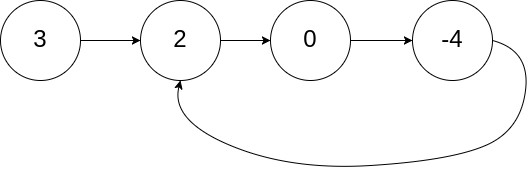
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
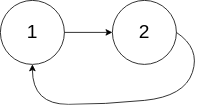
示例 2:
输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。

示例 3:
输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。
进阶:
你是否可以不用额外空间解决此题?
idea:fast,slow从head出发步长分别为2和1,第一次相遇让slow不动,fast从head开始,步长都变为1,第二次相遇的地方即为入环的第一个节点
证明
假设非环部分的长度是x,从环起点到相遇点的长度是y。环的长度是c。
现在走的慢的那个指针走过的长度肯定是x+n1*c+y,走的快的那个指针的速度是走的慢的那个指针速度的两倍。这意味着走的快的那个指针走的长度是2(x+n1*c+y)。
还有一个约束就是走的快的那个指针比走的慢的那个指针多走的路程一定是环长度的整数倍。根据上面那个式子可以知道2(x+n1*c+y)-x+n1*c+y=x+n1*c+y=n2*c。
所以有x+y=(n2-n1)*c,这意味着什么?我们解读下这个数学公式:非环部分的长度+环起点到相遇点之间的长度就是环的整数倍。这在数据结构上的意义是什么?现在我们知道两个指针都在离环起点距离是y的那个相遇点,而现在x+y是环长度的整数倍,这意味着他们从相遇点再走x距离就刚刚走了很多圈,这意味着他们如果从相遇点再走x就到了起点。
那怎么才能再走x步呢?答:让一个指针从头部开始走,另一个指针从相遇点走,等这两个指针相遇那就走了x步此时就是环的起点。
1 # Definition for singly-linked list. 2 # class ListNode(object): 3 # def __init__(self, x): 4 # self.val = x 5 # self.next = None 6 7 class Solution(object): 8 def detectCycle(self, head): 9 """ 10 :type head: ListNode 11 :rtype: ListNode 12 """ 13 fast,slow=head,head 14 while True: 15 if not fast or not fast.next:return 16 fast,slow = fast.next.next,slow.next 17 if fast == slow:break 18 fast = head 19 while fast!=slow: 20 fast,slow=fast.next,slow.next 21 return fast