已知双曲线(dfrac{x^2}{a^2}-dfrac{y^2}{b^2}=1) ((a>0,b>0))的左,右焦点分别为(F_1(-c,0)),(F_2(c,0)),直线(x=m)交双曲线于(A,B)两点,且(AF_2perp BF_1),(AF_2)与(y)轴的交点为(C(0,-3b)),则双曲线的离心率为((qquad))
(mathrm{A}.dfrac{3sqrt{5}}{5}) (qquadmathrm{B}.3) (qquadmathrm{C}.sqrt{3}+1) (qquadmathrm{D}.sqrt{2})
解析:
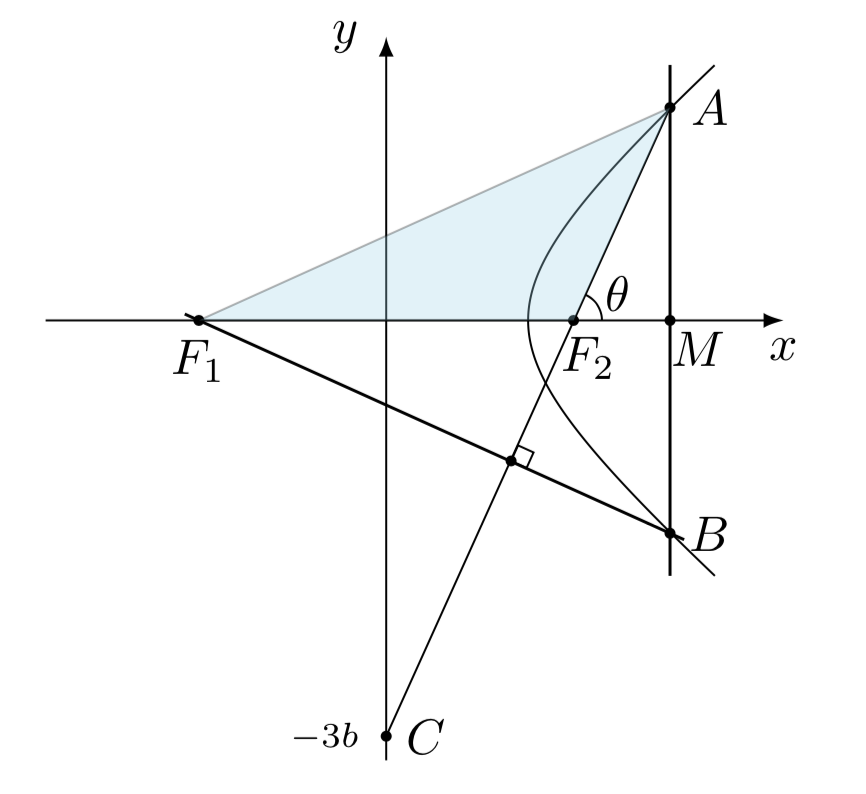
如图所示,若设$angle AF_2M= heta$,则$$ angle AF_1M=angle BF_1M=angle MAF_2=dfrac{pi}{2}- heta.$$于是在$ riangle AF_1F_2$中,$angle F_1AF_2=2 heta-dfrac{pi}{2}$.从而由正弦定理可得$$ dfrac{|F_1F_2|}{sinleft(2 heta-dfrac{pi}{2} ight)}=dfrac{|AF_1|}{sinleft(pi- heta ight)}=dfrac{|AF_2|}{sinleft(dfrac{pi}{2}- heta ight)}=dfrac{|AF_1|-|AF_2|}{sin heta-cos heta}.$$再结合双曲线的第一定义可知有$$dfrac{2c}{cos 2 heta}=dfrac{2a}{cos heta-sin heta}.$$从而离心率$e=cos heta+sin heta$.两边平方可得$$ dfrac{c^2}{c^2-b^2}=1+dfrac{ an heta}{1+ an^2 heta}=1+dfrac{dfrac{3b}{c}}{1+left(dfrac{3b}{c} ight)^2}.$$若设$t=dfrac{c}{b}$,则将上式整理可得$$ 6x^3-x^2-6x-9=0.$$ 易估计$2>x>1$,再结合有理根定理试根,只有$dfrac{3}{2}$满足,因此$x=dfrac{3}{2}$,从而所求离心率为$dfrac{3sqrt{5}}{5}$.