已知$A(-sqrt{3},0)$,(B(sqrt{3},0)),$P$为圆$x2+y2=1$上的动点,(overrightarrow{AP}=overrightarrow{PQ}),过点$P$作与$AP$垂直的直线$l$交直线$QB$于点$M$,则$M$的横坐标范围是$(qquad)$ (mathrm{A}. |x|geqslant 1) (qquadmathrm{B}. |x|> 1) (qquad mathrm{C}.|x|geqslant 2) (qquad mathrm{D}.|x|geqslant dfrac{sqrt{2}}{2}) 解析: 如图所示,容易知道
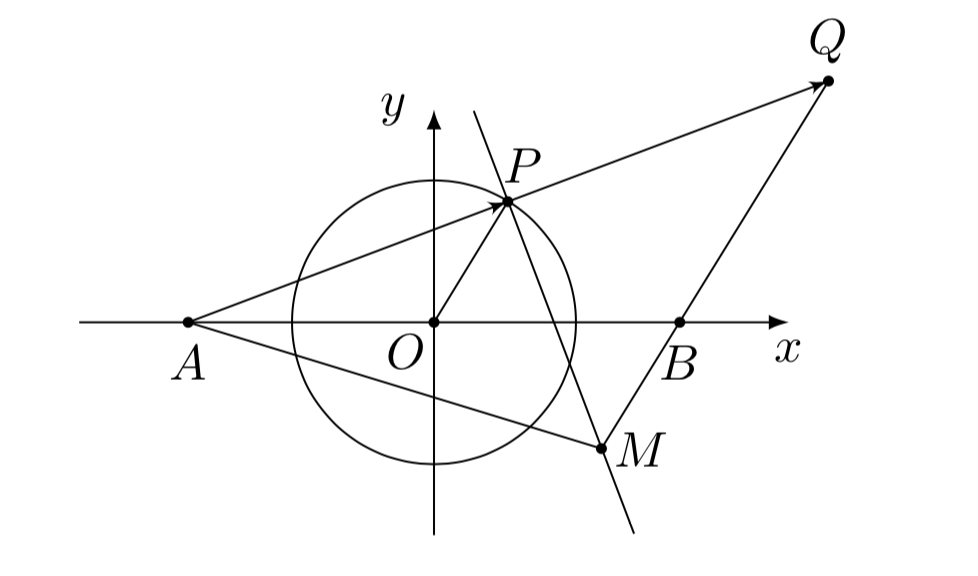
$PM$直线垂直平分$AQ$线段,因此$|AM|=|QM|$,并且根据位似知识容易知道$$ |QB|=2|OP|=2.$$从而$$ left ||MA|-|MB| ight |=left | |MQ|-|MB| ight |=|QB|=2.$$因此$M$点的轨迹是以$A,B$为左右焦点,以$(-1,0),(1,0)$为左右端点的双曲线上,从而$M$的横坐标的取值范围为$$|x|geqslant 1.$$