- 题目来源;
浙江大学在慕课网上开设的《数据结构》课,陈越老师、何钦铭老师主讲,课后作业的一道题。
- 题目描述:

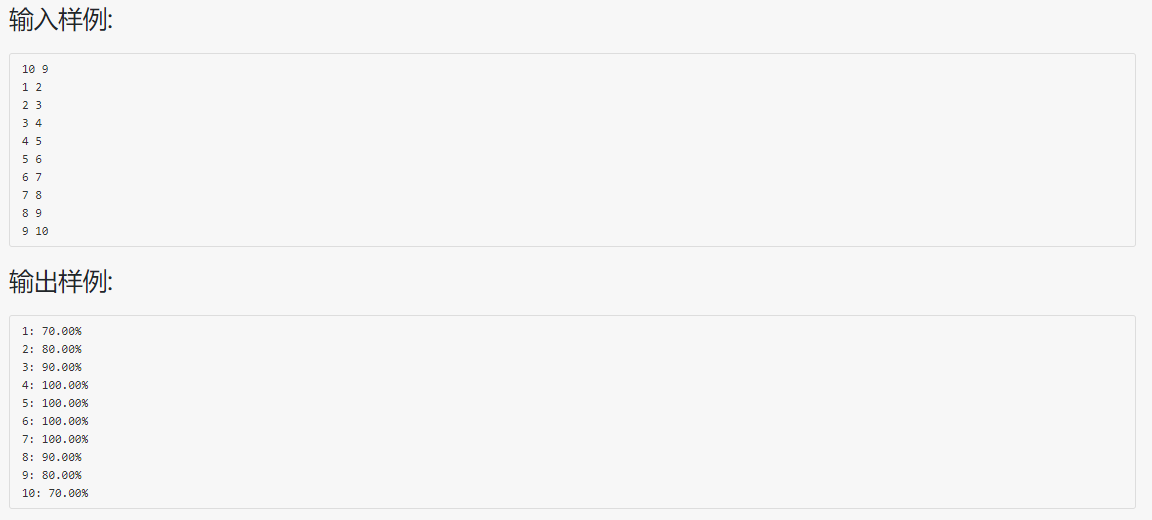
- 题目思路:
使用BFS即可。
- C语言实现
#define _CRT_SECURE_NO_WARNINGS
//使用邻接表来存储图
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// #include "queue.h"
/************************/
// #include "queue.h"
struct QNode
{
int* Data; //存储元素的数组
int Front; //队列的头指针
int Rear; //队列的尾指针
int MaxSize; //队列的最大容量
};
//创建一个队列
struct QNode* CreateQueue(int MaxSize)
{
struct QNode* Q = (struct QNode*)malloc(sizeof(struct QNode));
Q->Data = (int *)malloc(MaxSize * sizeof(int));
Q->Front = Q->Rear = 0;
Q->MaxSize = MaxSize;
return Q;
}
bool IsFull(struct QNode* Q)
{
return ((Q->Rear + 1) % Q->MaxSize) == Q->Front;
}
//在队列尾插入一个元素
//参数 struct QNode* Q 要操作的队列
// int x 待插入的元素
bool AddQ(struct QNode* Q, int x)
{
if (IsFull(Q)) //判断队列是否为空
{
printf("队列满,不能再插入元素
");
return false;
}
else
{
Q->Rear = (Q->Rear + 1) % Q->MaxSize;
Q->Data[Q->Rear] = x;
return true;
}
}
//判断队列是否为空
bool IsEmpty(struct QNode* Q)
{
return (Q->Front == Q->Rear);
}
//在队列头部删除一个元素
int DeleteQ(struct QNode* Q)
{
if (IsEmpty(Q))
{
printf("队列为空
");
return false;
}
else
{
Q->Front = (Q->Front + 1) % Q->MaxSize;
return Q->Data[Q->Front];
}
}
/****************************/
#define MaxVerterNum 1000
bool Visited[MaxVerterNum];
//边的定义
struct ENode
{
int V1;
int V2; //有向边<V1,V2>
int Weight; //权重
};
//邻接点的定义
struct AdjNode
{
int AdjV; //邻接点的下标
int Weight; //边的权值
struct AdjNode* Next; //指向下一个邻接点的指针
};
//顶点表头结点的定义
typedef struct Vnode
{
struct AdjNode* FirstEdge; //边表头指针
char Data; //存储顶点的数据 //这里设为字符型
}AdjList[MaxVerterNum];
//图节点的定义
struct GNode
{
int Nv; //顶点数
int Ne; //边数
AdjList G; //邻接表
};
struct GNode* CreateGraph(int VertexNum)
{
//初始化一个有VertexNum个顶点但没有边的图
int V;
struct GNode* Graph;
//建立图
Graph = (struct GNode*)malloc(sizeof(struct GNode));
Graph->Ne = 0;
Graph->Nv = VertexNum;
//初始化邻接表头指针
//这里默认顶点编号从0开始,到(Graph->Nv - 1)
for (V = 0; V < Graph->Nv;V++)
{
Graph->G[V].FirstEdge = NULL;
}
return Graph;
}
void InsertEdge(struct GNode* Graph,struct ENode* E)
{
struct AdjNode* NewNode;
NewNode = (struct AdjNode*)malloc(sizeof(struct AdjNode));
NewNode->AdjV = E->V2;
//NewNode->Weight = E->Weight;
NewNode->Weight = 1;
//将V2插入V1的表头
NewNode->Next = Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge = NewNode;
//若是无向图,还要插入边<V2,V1>
NewNode = (struct AdjNode*)malloc(sizeof(struct AdjNode));
NewNode->AdjV = E->V1;
//NewNode->Weight = E->Weight;
NewNode->Weight = 1;
//将V1插入V2的表头
NewNode->Next = Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge = NewNode;
}
struct GNode* BuildGraph()
{
struct GNode* Graph;
struct ENode* E;
int V;
int Nv, i;
scanf("%d",&Nv); //读入顶点的个数
Graph = CreateGraph(Nv); //初始化有Nv个顶点,但没有边的图
scanf("%d",&(Graph->Ne)); //读入边数
if (Graph->Ne != 0) //如果有边
{
//建立边节点
E = (struct ENode*)malloc(sizeof(struct ENode));
for (int i = 0;i < Graph->Ne;i++)
{
//读入格式为 起点 终点 权重
//scanf("%d %d %d",&E->V1,&E->V2,&E->Weight);
scanf("%d %d", &E->V1, &E->V2);
E->V1--;
E->V2--;
InsertEdge(Graph,E);
}
}
//如果顶点有数据的话,读入数据
//for (int i = 0; i < Graph->Nv;i++)
//{
// scanf("%c",&(Graph->G[i].Data));
//}
return Graph;
}
void InitializeVisited(int Nv)
{
int i = 0;
for (;i < Nv;i++)
{
Visited[i] = false;
}
}
int SDS_BFS(struct GNode* Graph,int S)
{
int V = 0;
int Tail = 0;
int Last = S;
int Level = 0;
int Count = 1;
struct AdjNode* W = NULL;
struct QNode* Q = CreateQueue(MaxVerterNum);
Visited[S] = true; //标记S已经被访问
AddQ(Q, S);
while (!IsEmpty(Q))
{
V = DeleteQ(Q);
for (W = Graph->G[V].FirstEdge; W ; W = W->Next)
{
if (!Visited[W->AdjV])
{
Visited[W->AdjV] = true; //标记W->AdjV已经被访问
//printf("%d.
",W->AdjV);
Count++;
Tail = W->AdjV; //当前的层尾
AddQ(Q, W->AdjV);
}
}
if (V == Last) //如果上一层的最后一个顶点弹出了
{
Level++;
Last = Tail;
}
if (Level == 6)
{
break;
}
}
return Count;
}
int main()
{
int count = 0;
struct GNode* Graph = BuildGraph();
for (int i = 0;i < Graph->Nv;i++)
{
InitializeVisited(Graph->Nv);
count = SDS_BFS(Graph,i);
printf("%d: %.2f%%
",i+1,100.0 * (double)count/(double)Graph->Nv);
}
// system("pause");
return 0;
}